อนุพันธ์

กราฟของฟังก์ชันแสดงด้วยเส้นสีดำ และเส้นสัมผัสแสดงด้วยเส้นสีแดง ความชันของเส้นสัมผัสมีค่าเท่ากับอนุพันธ์ของฟังก์ชันที่จุดสีแดง

{{#invoke:sidebar|collapsible | class = plainlist | titlestyle = padding-bottom:0.25em; | pretitle = บทความนี้เป็นส่วนหนึ่งของ | title = แคลคูลัส | image = $\underset{a}{\overset{b}{\int }}{f}^{\prime }(t)dt=f(b)-f(a)$ | listtitlestyle = text-align:center; | liststyle = border-top:1px solid #aaa;padding-top:0.15em;border-bottom:1px solid #aaa; | expanded = อนุพันธ์

| abovestyle = padding:0.15em 0.25em 0.3em;font-weight:normal; | above = ทฤษฎีบทมูลฐาน แม่แบบ:Startflatlist

• ลิมิตของฟังก์ชัน
• ความต่อเนื่อง

• ทฤษฎีบทค่าเฉลี่ย
• ทฤษฎีบทของโรลล์

| list2name = อนุพันธ์ | list2titlestyle = display:block;margin-top:0.65em; | list2title = แคลคูลัสเชิงอนุพันธ์ | list2 =

แม่แบบ:Sidebar

| list3name = ปริพันธ์ | list3title = แคลคูลัสเชิงปริพันธ์ | list3 =

แม่แบบ:Sidebar

| list4name = อนุกรม | list4title = อนุกรม | list4 =

แม่แบบ:Sidebar

| list5name = เวกเตอร์ | list5title = แคลคูลัสเวกเตอร์ | list5 =

แม่แบบ:Sidebar

| list6name = หลายตัวแปร | list6title = แคลคูลัสหลายตัวแปร | list6 =

แม่แบบ:Sidebar

| list7name = พิเศษ | list7title = พิเศษ | list7 = แม่แบบ:Startflatlist

• แคลคูลัสเชิงเศษส่วน
• มาลียาแว็ง
• แคลคูลัสเฟ้นสุ่ม
• แคลคูลัสของการแปรผัน

}}

ในวิชาคณิตศาสตร์ อนุพันธ์ (แม่แบบ:Langx) ของฟังก์ชันของตัวแปรจริง เป็นการวัดการเปลี่ยนแปลงของค่าของฟังก์ชันเทียบกับการเปลี่ยนแปลงของอาร์กิวเมนต์ (ค่าที่ป้อนเข้าหรือตัวแปรต้น) อนุพันธ์เป็นเครื่องมือพื้นฐานของแคลคูลัส ตัวอย่างเช่น อนุพันธ์ของตำแหน่งของวัตถุที่กำลังเคลื่อนที่เมื่อเทียบกับเวลา คือ ความเร็วของวัตถุนั้น ซึ่งเป็นการวัดว่าตำแหน่งของวัตถุมีการเปลี่ยนแปลงอย่างรวดเร็วเพียงใดเมื่อเวลาผ่านไป

อนุพันธ์ของฟังก์ชันตัวแปรเดียวที่ตัวแปรต้นใด ๆ คือความชันของเส้นสัมผัส (tangent) ที่สัมผัสกับกราฟของฟังก์ชันที่จุดนั้น เส้นสัมผัสคือการประมาณเชิงเส้นของฟังก์ชันที่ใกล้เคียงที่สุด (best linear approximation) กับค่าตัวแปรต้นนั้น ด้วยเหตุนี้ อนุพันธ์มักอธิบายได้ว่าเป็น "อัตราการเปลี่ยนแปลงขณะใดขณะหนึ่ง" ซึ่งก็คืออัตราส่วนของการเปลี่ยนแปลงขณะใดขณะหนึ่งของตัวแปรตามต่อตัวแปรต้นหรือตัวแปรอิสระ

กระบวนการหาอนุพันธ์เรียกว่า การหาอนุพันธ์ (differentiation หรือ การดิฟเฟอเรนชิเอต) ส่วนกระบวนการที่กลับกันเรียกว่า การหาปฏิยานุพันธ์ (antidifferentiation) ทฤษฎีบทมูลฐานของแคลคูลัสกล่าวว่าการหาปฏิยานุพันธ์เหมือนกันกับการหาปริพันธ์ (integration หรือ การอินทิเกรต) การหาอนุพันธ์และการหาปริพันธ์เป็นตัวดำเนินการพื้นฐานในแคลคูลัสตัวแปรเดียว

อนุพันธ์ของฟังก์ชันเป็นมโนทัศน์ (concept) หนึ่งในสองมโนทัศน์หลักของแคลคูลัส (อีกมโนทัศน์หนึ่งคือปฏิยานุพันธ์ ซึ่งคือตัวผกผันของอนุพันธ์)

นิยาม

โดยใช้ลิมิต

ฟังก์ชัน $f:ℝ\to ℝ$ ของตัวแปรจริงจะหาอนุพันธ์ได้ที่จุด $a$ ในโดเมนของฟังก์ชัน ถ้าโดเมนมีสับเซตเป็นช่วงเปิดที่มี $a$ เป็นสมาชิก และลิมิต

$L=\underset{h\to 0}{\lim }\frac{f(a+h)-f(a)}{h}$

หาค่าได้ หรืออีกนัยหนึ่ง สำหรับทุกจำนวนจริงบวก $\epsilon$ จะมีจำนวนจริงบวก $\delta$ ที่ทำให้ ทุกจำนวนจริง $h$ ที่ $|h|<\delta$ และ $h\ne 0$ แล้วจะได้ว่า $f(a+h)$ หาค่าได้และอสมการด้านล่างนี้เป็นจริง

$|L-\frac{f(a+h)-f(a)}{h}|<\epsilon$

โดยเส้นแนวตั้งในสมการข้างต้นแทนฟังก์ชันค่าสัมบูรณ์ นี่เป็นตัวอย่างหนึ่งของนิยาม (ε, δ) ของลิมิตแม่แบบ:Sfn

ถ้าฟังก์ชัน $f$ หาอนุพันธ์ได้ที่ $a$ นั่นคือถ้าลิมิต $L$ จากข้างต้นหาค่าได้ แล้วลิมิตนี้เรียกว่าอนุพันธ์ของ $f$ ที่ $a$ การเขียนอนุพันธ์เขียนได้หลายแบบแม่แบบ:Sfnm อนุพันธ์ของ $f$ ที่ $a$ สามารถเขียนเป็น $f^{\prime }(a)$ อ่านว่า "$f$ ไพรม์ของ $a$" หรือเขียนเป็น $\frac{df}{dx}(a)$ อ่านว่า "อนุพันธ์ของ $f$ เทียบ $x$ ที่ $a$" หรือ "ดีเอฟบายดีเอ็กซ์ที่เอ" ดู แม่แบบ:Slink ข้างล่าง

ตัวอย่าง ให้ $f$ เป็นฟังก์ชันกำลังสอง $f(x)=x^2$ แล้วผลหารในนิยามของอนุพันธ์คือแม่แบบ:Sfn

$\frac{f(a+h)-f(a)}{h}=\frac{(a+h{)}^2-a^2}{h}=\frac{a^2+2ah+h^2-a^2}{h}=2a+h$

การหารในขั้นตอนสุดท้ายถูกต้องก็ต่อเมื่อ $h\ne 0$ ยิ่ง h เข้าใกล้ $0$ มากเท่าไร ค่าของผลหารก็จะเข้าใกล้ $2a$ มากเท่านั้น พบว่าลิมิตหาค่าได้ และสำหรับทุก $a$ ลิมิตจะมีค่าเป็น $2a$ ดังนั้นอนุพันธ์ของฟังก์ชันกำลังสองคือ $f^{\prime }(x)=2x$

โดยใช้กณิกนันต์

อีกวิธีคิดหนึ่งของอนุพันธ์ $\frac{df}{dx}(a)$ คือเป็นอัตราส่วนของการเปลี่ยนแปลงกณิกนันต์ของฟังก์ชัน $f$ ต่อการเปลี่ยนแปลงกณิกนันต์ของฟังก์ชัน $x$แม่แบบ:Sfn การทำให้แนวคิดนี้รัดกุม จะต้องมีระบบกฎเกณฑ์ในการจัดการกับกณิกนันต์แม่แบบ:Sfn ระบบจำนวนไฮเพอร์เรียลสามารถจัดการกับปริมาณอนันต์และกณิกนันต์ได้ ไฮเพอร์เรียลเป็นส่วนขยายของจำนวนจริงที่มีจำนวนที่มากกว่าทุกสิ่งในรูป $1+1+\cdots +1$ สำหรับทุกพจน์จำกัด จำนวนดังกล่าวเป็นอนันต์ และส่วนกลับของมันเป็นกณิกนันต์ การประยุกต์ใช้ของจำนวนไฮเพอร์เรียลในรากฐานแคลคูลัสเรียกว่า การวิเคราะห์ที่ไม่มาตรฐาน เป็นการเปิดช่องให้นิยามแนวคิดพื้นฐานของแคลคูลัส เช่นอนุพันธ์ และปริพันธ์ ในรูปของกณิกนันต์ ให้ความหมายที่รัดกุมกับ $d$ ในสัญกรณ์ของไลบ์นิซ ดังนั้นอนุพันธ์ของ $f(x)$ จะกลายเป็น

$f^{\prime }(x)=\mathrm{st}\left(\frac{f(x+dx)-f(x)}{dx}\right)$

สำหรับทุกกณิกนันต์ $dx$ เมื่อ $\mathrm{st}$ หมายถึงฟังก์ชันส่วนมาตรฐาน ซึ่งปัดทุกไฮเพอร์เรียลจำกัดเป็นจำนวนจริงที่ใกล์ที่สุด เอาฟังก์ชันกำลังสอง $f(x)=x^2$ เป็นตัวอย่างอีกครั้ง

$\begin{array}{cc}{f}^{\prime }(x)& =\mathrm{st}\left(\frac{x^2+2x\cdot dx+(dx{)}^2-x^2}{dx}\right)\\ & =\mathrm{st}\left(\frac{2x\cdot dx+(dx{)}^2}{dx}\right)\\ & =\mathrm{st}(\frac{2x\cdot dx}{dx}+\frac{(dx{)}^2}{dx})\\ & =\mathrm{st}(2x+dx)\\ & =2x.\end{array}$

การหาอนุพันธ์และอนุพันธ์

การหาอนุพันธ์ เป็นการคำนวณเพื่อที่จะได้มาซึ่งอนุพันธ์ อนุพันธ์ของฟังก์ชัน แม่แบบ:Math ของตัวแปร แม่แบบ:Math คืออัตราที่ค่า แม่แบบ:Math ของฟังก์ชันเปลี่ยนแปลงไปต่อการเปลี่ยนแปลงของตัวแปร แม่แบบ:Math เรียกว่า อนุพันธ์ของ แม่แบบ:Math เทียบกับ แม่แบบ:Math ถ้า แม่แบบ:Math และ แม่แบบ:Math เป็นจำนวนจริง และถ้ากราฟของฟังก์ชัน แม่แบบ:Math ลงจุดเทียบกับ แม่แบบ:Math อนุพันธ์ก็คือความชันของเส้นกราฟในแต่ละจุด

ความชันของฟังก์ชันเชิงเส้น: $m=\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}$

กรณีที่ง่ายที่สุด นอกเหนือจากกรณีของฟังก์ชันคงตัว คือเมื่อ แม่แบบ:Math เป็นฟังก์ชันเชิงเส้นของ แม่แบบ:Math ซึ่งหมายถึงกราฟของ แม่แบบ:Math จะเป็นเส้นตรง ในกรณีนี้ แม่แบบ:Math สำหรับจำนวนจริง แม่แบบ:Math และ แม่แบบ:Math และความชัน แม่แบบ:Math ซึ่งกำหนดโดยการเปลี่ยนแปลงของ แม่แบบ:Math หารด้วยการเปลี่ยนแปลงของ แม่แบบ:Math ดังสมการ

$m=\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}$

เมื่อสัญลักษณ์ แม่แบบ:Math (เดลตา) แทนคำว่า "การเปลี่ยนแปลง" สูตรนี้เป็นจริง เพราะว่า

$y+\mathrm{\Delta }y=f(x+\mathrm{\Delta }x)=m(x+\mathrm{\Delta }x)+b=mx+m\mathrm{\Delta }x+b=y+m\mathrm{\Delta }x$

เพราะฉะนั้น จะได้

$y+\mathrm{\Delta }y=y+m\mathrm{\Delta }x$

ทำให้ได้

$\mathrm{\Delta }y=m\mathrm{\Delta }x$

ซึ่ง แม่แบบ:Math เป็นค่าที่ถูกต้องของความชันของเส้นกราฟ ถ้าฟังก์ชัน แม่แบบ:Math ไม่เป็นฟังก์ชันเชิงเส้น (กล่าวคือ กราฟของมันไม่เป็นเส้นตรง) แล้วการเปลี่ยนแปลงของ แม่แบบ:Math หารด้วยการเปลี่ยนแปลงของ แม่แบบ:Math จะมีค่าแตกต่างกันออกไป การหาอนุพันธ์จึงเป็นวิธีการที่จะหาค่าที่ถูกต้องของอัตราการเปลี่ยนแปลงที่ค่าตัวแปรต้น แม่แบบ:Math ใด ๆ

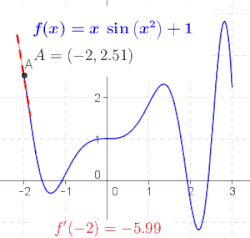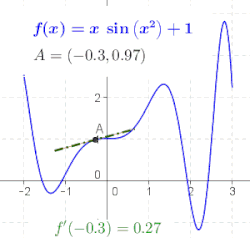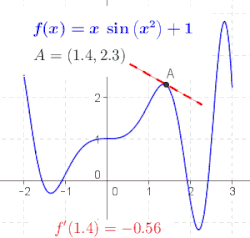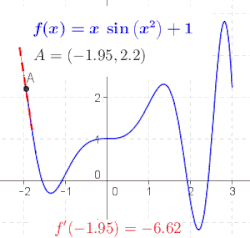
แนวคิดนี้ ซึ่งแสดงดังรูปที่ 1 ถึงรูปที่ 3 คือการคำนวณอัตราการเปลี่ยนแปลงจากค่าลิมิตของอัตราส่วนของผลต่าง แม่แบบ:Math เมื่อ แม่แบบ:Math เข้าใกล้ค่าที่น้อยมาก

สัญกรณ์

แม่แบบ:บทความหลัก มีสัญกรณ์สำหรับอนุพันธ์สองแบบที่ใช้กันโดยทั่วไป แบบหนึ่งมาจากไลบ์นิซ และอีกแบบหนึ่งมาจากลากรางจ์ อนุพันธ์อีกแบบหนึ่งซึ่งคิดขึ้นโดยนิวตันมีใช้บ้างในสาขาฟิสิกส์

ในสัญกรณ์ของไลบ์นิซ การเปลี่ยนแปลงที่น้อยมากของ แม่แบบ:Math แสดงได้เป็น แม่แบบ:Math และอนุพันธ์ของ แม่แบบ:Math เทียบกับ แม่แบบ:Math เขียนได้ดังนี้

$\frac{dy}{dx}$

แสดงถึงอัตราส่วนของปริมาณที่น้อยมากสองปริมาณ (ข้างบนอ่านว่า "อนุพันธ์ของ y เทียบกับ x" หรือ "d y บาย d x" รูปแบบ "d y d x" นี้ใช้กันในการสนทนาอย่างบ่อยครั้ง แต่มันอาจทำให้สับสนได้)

ส่วนสัญกรณ์ของลากรางจ์ อนุพันธ์ของฟังก์ชัน แม่แบบ:Math เทียบกับ แม่แบบ:Math แสดงได้เป็น แม่แบบ:Math (อ่านว่า "f ไพรม์ของ of x") หรือ แม่แบบ:Math (อ่านว่า "f ไพรม์ x ของ x")

และในสัญกรณ์ของนิวตัน อนุพันธ์ของฟังก์ชันเขียนแทนด้วยจุดบนตัวแปรตาม นั่นคือ ถ้า y เป็นฟังก์ชันของ t แล้วอนุพันธ์ของ y เทียบกับ t จะเขียนแทนด้วย $\dot{y}$ ในขณะที่อนุพันธ์อันดับที่สูงขึ้นจะเพิ่มจำนวนจุด เช่น $\ddot{y},\stackrel{...}{y}$ สัญกรณ์นี้นิยมใช้สำหรับตัวแปรตามที่ขึ้นกับเวลา

อัตราส่วนเชิงผลต่างของนิวตัน

เส้นตัดเข้าใกล้เส้นสัมผัสเมื่อ $\mathrm{\Delta }x\to 0$

อนุพันธ์ของฟังก์ชัน f ที่ x ในเชิงเรขาคณิต คือ ความชันของเส้นสัมผัสของกราฟ f ที่ x เราไม่สามารถหาความชันของเส้นสัมผัสจากฟังก์ชันที่กำหนดให้โดยตรงได้ เพราะว่าเรารู้เพียงจุดบนเส้นสัมผัส ซึ่งก็คือ (x, f (x)) เท่านั้น ในทางอื่น เราจะประมาณความชันของเส้นสัมผัสด้วยเส้นตัด (secant line) หลาย ๆ เส้น ที่มีจุดตัดทั้ง 2 จุดอยู่ห่างกันเป็นระยะทางสั้น ๆ เมื่อหาลิมิตของความชันของเส้นตัดที่จุดตัดอยู่ใกล้กันมาก ๆ เราจะได้ความชันของเส้นสัมผัส ดังนั้น อาจนิยามอนุพันธ์ว่าคือ ลิมิตของความชันของเส้นตัดที่เข้าใกล้เส้นสัมผัส

เพื่อหาความชันของเส้นตัดที่จุดตัดอยู่ใกล้กันมาก ๆ ให้ h เป็นจำนวนที่มีค่าน้อย ๆ h จะแทนการเปลี่ยนแปลงน้อย ๆ ใน x ซึ่งจะเป็นจำนวนบวกหรือลบก็ได้ ดังนั้น ความชันของเส้นที่ลากผ่านจุด (x,f (x) ) และ (x+h,f (x+h) ) คือ

$\frac{f(x+h)-f(x)}{h}$

ซึ่งนิพจน์นี้ก็คือ อัตราส่วนเชิงผลต่างของนิวตัน (Newton's difference quotient) อนุพันธ์ของ f ที่ x คือ ลิมิตของค่าของผลหารเชิงผลต่าง ของเส้นตัดที่เข้าใกล้กันมาก ๆ จนเป็นเส้นสัมผัส:

$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$

ตัวอย่าง

ฟังก์ชันกำลังสอง

ฟังก์ชันกำลังสอง แม่แบบ:Math หาอนุพันธ์ได้ที่ แม่แบบ:Math และอนุพันธ์ของมันที่ตำแหน่งนั้นเท่ากับ 6 ผลลัพธ์นี้มาจากการคำนวณลิมิตของอัตราส่วนของผลต่างของ แม่แบบ:Math เมื่อ แม่แบบ:Math เข้าใกล้ศูนย์:

$\begin{array}{cc}{f}^{\prime }(3)& =\underset{h\to 0}{\lim }\frac{f(3+h)-f(3)}{h}=\underset{h\to 0}{\lim }\frac{(3+h{)}^2-3^2}{h}\\ & =\underset{h\to 0}{\lim }\frac{9+6h+h^2-9}{h}=\underset{h\to 0}{\lim }\frac{6h+h^2}{h}=\underset{h\to 0}{\lim }(6+h)\end{array}$

นิพจน์สุดท้ายแสดงให้เห็นว่าอัตราส่วนของผลต่างเท่ากับ แม่แบบ:Math เมื่อ แม่แบบ:Math และไม่นิยามเมื่อ แม่แบบ:Math เนื่องจากนิยามของอัตราส่วนของผลต่าง อย่างไรก็ตาม นิยามของลิมิตกล่าวว่าอัตราส่วนของผลต่างไม่จำเป็นต้องนิยามเมื่อ แม่แบบ:Math ลิมิตก็คือผลลัพธ์จากการให้ แม่แบบ:Math เข้าสู่ศูนย์ ซึ่งหมายถึงแนวโน้มของค่า แม่แบบ:Math เมื่อ แม่แบบ:Math มีค่าน้อยลงมาก ๆ

$\underset{h\to 0}{\lim }(6+h)=6+0=6$

ดังนั้น ความชันของกราฟของฟังก์ชันกำลังสองที่จุด แม่แบบ:Nowrap คือ 6 และอนุพันธ์ของมันที่ แม่แบบ:Math คือ แม่แบบ:Math

ต่อไปนี้เป็นการคำนวณในทำนองเดียวกันในกรณีทั่วไป ซึ่งแสดงให้เห็นว่าอนุพันธ์ของฟังก์ชันกำลังสองที่ แม่แบบ:Math คือ แม่แบบ:Math:

$\begin{array}{cc}{f}^{\prime }(a)& =\underset{h\to 0}{\lim }\frac{f(a+h)-f(a)}{h}=\underset{h\to 0}{\lim }\frac{(a+h{)}^2-a^2}{h}\\ & =\underset{h\to 0}{\lim }\frac{a^2+2ah+h^2-a^2}{h}=\underset{h\to 0}{\lim }\frac{2ah+h^2}{h}\\ & =\underset{h\to 0}{\lim }(2a+h)=2a\end{array}$

ความต่อเนื่องและการหาอนุพันธ์ได้

ถ้า f เป็นฟังก์ชันที่หาอนุพันธ์ ณ a ได้ f จะต้องต่อเนื่องที่ a เสมอ ถ้า f ไม่ต่อเนื่องที่ a จะหาอนุพันธ์ไม่ได้ ตัวอย่างเช่น เลือกจุด a และให้ f เป็นฟังก์ชันขั้นบันไดที่มีค่า 1 สำหรับ x ทั้งหมดที่น้อยกว่า a และมีค่า 10 สำหรับ x ทั้งหมดที่มากกว่าหรือเท่ากับ a แล้ว f ไม่สามารถมีอนุพันธ์ได้ที่ a โดยหาก h เป็นค่าลบ a + h จะอยู่ที่ส่วนล่างของขั้นบันได ดังนั้นเส้นตัดจาก a ถึง a + h นั้นสูงชันมากและเมื่อ h มีแนวโน้มเป็นศูนย์ความชันจะไม่มีที่สิ้นสุด หาก h เป็นค่าบวก a + h จะอยู่บนส่วนสูงของขั้นบันได ดังนั้นเส้นตัดจาก a ถึง a + h มีความชันเป็นศูนย์ ดังนั้นเส้นตัดจึงไม่ได้เข้าใกล้ความชันเดียว และลิมิตของอัตราส่วนของผลต่างจึงไม่สามารถหาได้

อย่างไรก็ตาม ถึงแม้ว่าฟังก์ชันจะต่อเนื่อง ณ จุดหนึ่ง ก็ยังอาจไม่สามารถหาอนุพันธ์ได้ ตัวอย่างเช่นฟังก์ชันค่าสัมบูรณ์ f(x) = |x| ต่อเนื่องที่ x = 0 แต่ไม่สามารถหาอนุพันธ์ได้ หาก h เป็นค่าบวกความชันของเส้นตัดจาก 0 ถึง h จะเท่ากับ 1 ในขณะที่ถ้า h เป็นลบความชันของเส้นตัดจาก 0 ถึง h จะเป็น -1 จุดที่หาอนุพันธ์ไม่ได้นี้สามารถเห็นได้ชัดเจนว่าเป็นมุมในกราฟที่ x = 0 แต่แม้ฟังก์ชันที่กราฟไม่หักมุมก็ยังอาจจะไม่สามารถหาอนุพันธ์ได้ ณ จุดที่ความชันเป็นแนวตั้ง: ตัวอย่างเช่นฟังก์ชันที่กำหนดโดย f(x) = x^1/3 ไม่สามารถหาอนุพันธ์ได้ที่ x = 0

สรุปว่า ฟังก์ชันที่มีอนุพันธ์นั้นต่อเนื่อง แต่มีฟังก์ชันต่อเนื่องที่ไม่มีอนุพันธ์

ฟังก์ชันส่วนใหญ่ที่พบในทางปฏิบัติมีอนุพันธ์ทุกจุดหรือเกือบทุกจุด เพราะเหตุนี้ ในช่วงแรกของประวัติศาสตร์ของแคลคูลัส นักคณิตศาสตร์หลายคนสันนิษฐานว่าฟังก์ชันต่อเนื่องมีอนุพันธ์ที่จุดส่วนใหญ่ ซึ่งภายใต้เงื่อนไขที่ไม่รุนแรงมาก เช่นถ้าฟังก์ชันเป็นฟังก์ชันโมโนโทนหรือฟังก์ชันลิปชิตส์ สิ่งนี้จะเป็นจริง อย่างไรก็ตามในปี 1872 ไวเออร์ชตราส พบตัวอย่างแรกของฟังก์ชันที่ต่อเนื่องได้ทุกที่ แต่ไม่สามารถหาอนุพันธ์ได้ที่ไหน ตัวอย่างนี้เรียกว่าฟังก์ชันไวเออร์ชตราส ในปี 1931 สเตฟาน บานาค พิสูจน์ว่าเซตของฟังก์ชันที่มีอนุพันธ์ในบางจุดเป็นเพียงส่วนเล็ก ๆ ของฟังก์ชันต่อเนื่องทั้งหมด หมายความว่าการสุ่มฟังก์ชันต่อเนื่องใด ๆ แทบไม่มีโอกาสเลยที่จะหาอนุพันธ์ได้แม้จุดเดียว

อนุพันธ์ในฐานะฟังก์ชัน

ถ้าฟังก์ชัน f สามารถหาค่าอนุพันธ์ได้ในทุกจุดในโดเมนของมัน เราสามารถนิยามฟังก์ชันที่พาค่า x ทุกค่าในโดเมนนั้นไปหาค่าของอนุพันธ์ของ f ที่ x ได้ ฟังก์ชันนี้เขียนแทนด้วย f' และเรียกว่า ฟังก์ชันอนุพันธ์ ของ f

ในกรณีที่ f ไม่สามารถหาอนุพันธ์ได้ครบทุกจุดในโดเมน ฟังก์ชันที่มีค่าเท่ากับอนุพันธ์นี้สำหรับจุดที่หาได้ และไม่นิยามสำหรับจุดอื่น ๆ ก็สามารถเรียกว่าอนุพันธ์ของ f ได้เช่นกัน ซึ่งอนุพันธ์นี้ยังคงเป็นฟีงก์ชัน แต่มีโดเมนเล็กกว่า f

จากมุมมองนี้ เราสามารถมองการหาอนุพันธ์เป็นฟังก์ชันของฟังก์ชัน นั่นคือ อนุพันธ์เป็นตัวดำเนินการที่มีโดเมนเป็นเซตของฟังก์ชันทุกฟังก์ชันที่หาอนุพันธ์ได้ทุกจุดบนโดเมนของตัวมันเอง และมีเรนจ์เป็นเซตของฟังก์ชัน หากเราแทนตัวดำเนินการนี้ด้วย D แล้วจะได้ D(f) = f' เนื่องจาก D(f) เป็นฟังก์ชัน สามารถหาค่าที่จด a ใด ๆ ได้ว่า D(f)(a) = f'(a)

แสดงความชันในแต่ละจุดของฟังก์ชัน $f(x)=1+x\sin x^2$ ซึ่งจะสังเกตเห็นได้ว่าเส้นที่แสดงความชันที่จุดใดๆจะสัมผัส (tangent) กับกราฟของฟังก์ชันที่จุดนั้นๆ ความชันในที่นี้ก็คืออนุพันธ์ของฟังก์ชันนั้นเอง หมายเหตุ สีเขียว คือ ความชันเป็นบวก สีแดง คือ ความชันเป็นลบ สีดำ คือ ความชันเป็นศูนย์

อนุพันธ์อันดับสูง

หาก f เป็นฟังก์ชันที่หาอนุพันธ์ได้ โดย f' เป็นอนุพันธ์ของ f แล้วอนุพันธ์ของ f' อีกทีหนึ่ง (ถ้าอนุพันธ์นี้หาได้) เขียนแทนด้วย f'' และเรียกว่า อนุพันธ์อันดับสอง ของ f ในทำนองเดียวกัน อนุพันธ์ของ f'' (ถ้าหาได้) เขียนแทนด้วย f''' และเรียกว่า อนุพันธ์อันดับสาม ของ f เมื่อทำเช่นนี้ซ้ำไปเรื่อย ๆ เราก็จะได้นิยามของ อนุพันธ์อันดับที่ n ว่าเป็นอนุพันธ์ของอนุพันธ์อันดับที่ n - 1 อนุพันธ์อันดับตั้งแต่สองขึ้นไปนี้โดยรวมเรียกว่า อนุพันธ์อันดับสูง (แม่แบบ:Langx)

อนุพันธ์อันดับสูงมีนัยสำคัญในวิชาฟิสิกส์ กล่าวคือ ถ้า x(t) แสดงตำแหน่งของวัตถุที่เวลา t แล้วอนุพันธ์อันดับหนึ่งของ x แสดงความเร็วของวัตถุ และอันดับสองแสดงความเร่ง

ฟังก์ชันที่มีอนุพันธ์ไม่จำเป็นต้องมีอนุพันธ์อันดับสูงกว่านั้น เช่น หาก

$f(x)=\{\begin{array}{cc}+x^2,& x\ge 0\\ -x^2,& x\le 0\end{array}$

แล้วจะสามารถพิสูจน์ได้ว่า f หาอนุพันธ์ได้เท่ากับ

$f^{\prime }(x)=\{\begin{array}{cc}+2x,& x\ge 0\\ -2x,& x\le 0\end{array}$

เท่ากับสองเท่าของฟังก์ชันค่าสัมบูรณ์ ซึ่งไม่มีอนุพันธ์ที่ x = 0 ดังนั้น f ไม่มีอนุพันธ์อันดับสองที่ค่า x นี้

ในทำนองเดียวกัน ฟังก์ชันสามารถมีอนุพันธ์ขึ้นไปถึงอันดับที่ k แต่ไม่มีอนุพันธ์อันดับที่ k + 1 ซึ่งเรียกว่าฟังก์ชันที่หาอนุพันธ์ได้ k ครั้ง และถ้าอนุพันธ์อันดับที่ k นี้ต่อเนื่องด้วย จะเรียกฟังก์ชันนั้นว่าอยู่ในคลาส C^k ฟังก์์ชันที่หาอนุพันธ์ได้เรื่อย ๆ โดยไม่จำกัดครั้งเรียกว่า ฟังก์ชันปรับเรียบ (แม่แบบ:Langx)

ฟังก์ชันพหุนามทุกฟังก์ชันสามารถหาอนุพันธ์ได้ไม่จำกัดครั้ง โดยถ้าพหุนามดีกรี n ถูกหาอนุพันธ์ n ครั้งจะได้ฟังก์ชันค่าคงที่เสมอ และอนุพันธ์อันดับถัดจากนั้นก็จะเป็นศูนย์ทุกอันดับ ดังนั้นฟังก์ชันพหุนามทุกฟังก์ชันเป็นฟังก์ชันปรับเรียบ

จุดเปลี่ยนเว้า

แม่แบบ:บทความหลัก จุดที่อนุพันธ์อันดับสองของฟังก์ชันเปลี่ยนเครื่องหมาย (จากจำนวนจริงลบเป็นจำนวนจริงบวก หรือในทางกลับกัน) เรียกว่า จุดเปลี่ยนเว้า ที่จุดเปลี่ยนเว้า อนุพันธ์อันดับสองอาจเป็นศูนย์ ดังในกรณีที่จุดเปลี่ยนเว้าที่ แม่แบบ:Math ของฟังก์ชัน แม่แบบ:Math หรืออนุพันธ์อันดับสองอาจหาค่าไม่ได้ ดังในกรณีที่จุดเปลี่ยนเว้าที่ แม่แบบ:Math ของฟังก์ชัน แม่แบบ:Math ฟังก์ชันจะเปลี่ยนจากฟังก์ชันเว้าไปเป็นฟังก์ชันนูนหรือในทางกลับกันที่จุดเปลี่ยนเว้า

รายละเอียดสัญกรณ์

สัญกรณ์ของไลบ์นิซ

สัญลักษณ์ dx, dy และ dx/dy เสนอโดยกอทท์ฟรีด วิลเฮล์ม ไลบ์นิซ ใน ค.ศ. 1675 สัญลักษณ์นี้ใช้กันอย่างทั่วไปเมื่อสมการ แม่แบบ:Nowrap ซึ่งแสดงถึงความสัมพันธ์เชิงฟังก์ชันระหว่างตัวแปรต้นและตัวแปรตาม อนุพันธ์อันดับหนึ่งเขียนได้ดังนี้

$\frac{dy}{dx},\frac{df}{dx}(x),\mathrm{o}\mathrm{r}\frac{d}{dx}f(x)$

อนุพันธ์อันดับสูงจะแสดงโดยใช้สัญลักษณ์

$\frac{d^{n}y}{d{x}^n},\frac{d^{n}f}{d{x}^n}(x),\mathrm{o}\mathrm{r}\frac{d^n}{d{x}^n}f(x)$

สำหรับอนุพันธ์อันดับที่ n ของ แม่แบบ:Nowrap (เทียบกับ x) ข้างบนเป็นสัญลักษณ์ย่อของการใช้ตัวดำเนินการอนุพันธ์หลายตัว ยกตัวอย่างเช่น

$\frac{d^{2}y}{d{x}^2}=\frac{d}{dx}\left(\frac{dy}{dx}\right)$

ในสัญกรณ์ของไลบ์นิซ เราสามารถเขียนอนุพันธ์ของ y ที่จุด แม่แบบ:Nowrap ในรูปที่แตกต่างกันสองแบบ:

${\frac{dy}{dx}|}_{x=a}=\frac{dy}{dx}(a)$

สัญกรณ์ของไลบ์นิซช่วยให้สามารถระบุตัวแปรในการหาอนุพันธ์ได้ (ในตัวส่วน) โดยเฉพาะในเรื่องการหาอนุพันธ์ย่อย และยังทำให้ง่ายต่อการจำกฎลูกโซ่อีกด้วย:

$\frac{dy}{dx}=\frac{dy}{du}\cdot \frac{du}{dx}.$

สัญกรณ์ของลากรางจ์

ในบางครั้งเราเรียกว่า สัญกรณ์ไพรม์ หนึ่งในสัญกรณ์ยุคใหม่ที่ใช้กันมากที่สุดสำหรับการหาอนุพันธ์ ซึ่งมาจากโฌแซ็ฟ-หลุยส์ ลากร็องฌ์ โดยใช้เครื่องหมายไพรม์ กล่าวคือ อนุพันธ์ของฟังก์ชัน f(x) เขียนได้ในรูป f′(x) หรือ f′ ในทำนองเดียวกันอนุพันธ์อันดับสองและสามก็เขียนได้ในรูปดังนี้

$(f^{\prime }{)}^{\prime }=f^{″}$   และ   $(f^{″}{)}^{\prime }=f^{‴}$

เพื่อที่จะเขียนอนุพันธ์อันดับที่สูงกว่านี้ ผู้เขียนบางคนก็จะใช้เลขโรมันเป็นตัวยก หรือบางคนอาจใช้จำนวนนับในวงเล็บ:

$f^{\mathrm{i}\mathrm{v}}$   หรือ   $f^{(4)}$

สัญกรณ์ด้านหลัง ถ้าอยู่ในรูปทั่วไปก็คือ f ⁽ⁿ⁾ สำหรับอนุพันธ์อันดับ n ของ f สัญกรณ์นี้มีประโยชน์มากที่สุดเมื่อเราต้องการจะกล่าวถึงอนุพันธ์ในอยู่ในรูปฟังก์ชันของมันเอง ดังเช่นในกรณีนี้ สัญกรณ์ไลบ์นิซอาจกลายเป็นเรื่องยุ่งยาก

สัญกรณ์ของนิวตัน

สัญกรณ์ของนิวตันสำหรับการหาอนุพันธ์ เรียกได้อีกอย่างหนึ่งว่าสัญกรณ์จุด โดยการเขียนไว้เหนือชื่อฟังก์ชันเพื่อแทนจำนวนครั้งของอนุพันธ์ ถ้า แม่แบบ:Nowrap แล้ว

$\dot{y}$   และ   $\ddot{y}$

หมายถึง อนุพันธ์อันดับหนึ่งและสองของ y เทียบกับ t ตามลำดับ สัญกรณ์นี้นำไปใช้อย่างเฉพาะทางอย่างเช่น อนุพันธ์เทียบกับเวลา หรือเทียบกับความยาวส่วนโค้ง ซึ่งใช้กันทั่วไปในฟิสิกส์ สมการเชิงอนุพันธ์ และเรขาคณิตเชิงอนุพันธ์ โดยสัญกรณ์นี้ไม่สามารถที่จะเขียนได้เมื่ออนุพันธ์มีอันดับที่สูงขึ้น ในทางปฏฺบัติ จะใช้เพียงอนุพันธ์ไม่กี่อันดับที่จำเป็นเท่านั้น

สัญกรณ์ของออยเลอร์

สัญกรณ์ของออยเลอร์จะใช้ตัวดำเนินการเชิงอนุพันธ์ D ซึ่งจะใช้กับฟังก์ชัน f เพื่อที่จะได้อนุพันธ์อันดับหนึ่ง Df ส่วนอนุพันธ์อันดับสองเขียนได้ในรูป D²f และอนุพันธ์อันดับ n เขียนได้ในรูป Dⁿf

ถ้า แม่แบบ:Nowrap เป็นตัวแปรตาม แล้ว x จะเป็นตัวห้อยอยู่ใต้ D เพื่อบ่งบอกว่ากำลังเทียบกับตัวแปรต้น x ดังข้างล่าง

$D_{x}y$   หรือ $D_{x}f(x)$,

แต่ตัวห้อย x มักจะถูกละไว้ในฐานที่เข้าใจเพื่อความรวดเร็ว เมื่อมีตัวแปรต้นนี้อยู่ตัวเดียว

สัญกรณ์ของออยเลอร์มีประโยชน์ในการแก้สมการเชิงอนุพันธ์เชิงเส้น

กฎการคำนวณ

กฎสำหรับฟังก์ชันพื้นฐาน

• การหาอนุพันธ์ของเลขยกกำลัง: ถ้า

$f(x)=x^r$

เมื่อ r เป็นจำนวนจริงใด ๆ แล้ว

$f^{\prime }(x)=r{x}^{r-1}$

เมื่อไรก็ตามที่ฟังก์ชันนี้สามารถหาค่าได้ ตัวอย่างเช่น ถ้า $f(x)=x^{1/4}$ แล้ว

$f^{\prime }(x)=(1/4)x^{-3/4}$

และฟังก์ชันอนุพันธ์สามารถหาค่าได้เฉพาะสำหรับค่า x ที่เป็นบวก ไม่ใช่ แม่แบบ:Nowrap เมื่อ แม่แบบ:Nowrap กฎนี้จะให้ค่า f′(x) เป็นศูนย์สำหรับ แม่แบบ:Nowrap ซึ่งกรณีนี้ก็คือกฎค่าคงที่

• กฎค่าคงที่: ถ้า f(x) คือค่าคงที่ แล้ว

$f^{\prime }=0$

• ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม:

$\frac{d}{dx}{e}^x=e^x$

$\frac{d}{dx}{a}^x=a^x\ln (a)$

$\frac{d}{dx}\ln (x)=\frac{1}{x},x>0$

$\frac{d}{dx}{\log }_a(x)=\frac{1}{x\ln (a)}$

• ฟังก์ชันตรีโกณมิติ:

$\frac{d}{dx}\sin (x)=\cos (x)$

$\frac{d}{dx}\cos (x)=-\sin (x)$

$\frac{d}{dx}\tan (x)={\sec }^2(x)=\frac{1}{{\cos }^2(x)}=1+{\tan }^2(x)$

จากกฎผลคูณและกฎผลหารทำให้ได้

$\frac{d}{dx}\csc (x)=-\csc x\cot x$

$\frac{d}{dx}\sec (x)=\sec x\tan x$

$\frac{d}{dx}\cot (x)=-{\csc }^{2}x$

• ฟังก์ชันตรีโกณมิติผกผัน:

$\frac{d}{dx}\arcsin (x)=\frac{1}{\sqrt{1-x^2}},-1<x<1$

$\frac{d}{dx}\arccos (x)=-\frac{1}{\sqrt{1-x^2}},-1<x<1$

$\frac{d}{dx}\arctan (x)=\frac{1}{1+x^2}$

กฎสำหรับฟังก์ชันหลายฟังก์ชันรวมกัน

ในหลายกรณี การใช้วิธีอัตราส่วนเชิงผลต่างของนิวตันแบบตรง ๆ จะทำให้การคำนวณลิมิตยุ่งยากได้ ซึ่งหลีกเลี่ยงโดยการใช้กฎการหาอนุพันธ์เหล่านี้

• กฎผลรวม:

$(\alpha f+\beta g{)}^{\prime }=\alpha f^{\prime }+\beta g^{\prime }$ สำหรับฟังก์ชันทั้งหมด f และ g และจำนวนจริงทั้งหมด $\alpha$ และ $\beta$

• กฎผลคูณ:

$(fg{)}^{\prime }=f^{\prime }g+f{g}^{\prime }$ สำหรับฟังก์ชันทั้งหมด f และ g ในกรณีพิเศษ กฎนี้รวมถึงข้อเท็จจริงที่ว่า $(\alpha f{)}^{\prime }=\alpha f^{\prime }$ เมื่อไรก็ตามที่ $\alpha$ เป็นค่าคงที่ เพราะว่า ${\alpha }^{\prime }f=0\cdot f=0$ จากกฎค่าคงที่

• กฎผลหาร:

$\left(\frac{f}{g}\right)=\frac{f^{\prime }g-f{g}^{\prime }}{g^2}$ สำหรับฟังก์ชันทั้งหมด f และ g ของตัวแปรต้นทั้งหมดโดยที่ แม่แบบ:Nowrap.

• กฎลูกโซ่: ถ้า $f(x)=h(g(x))$ แล้ว

$f^{\prime }(x)=h^{\prime }(g(x))\cdot g^{\prime }(x)$

ตัวอย่างการคำนวณ

อนุพันธ์ของ

$f(x)=x^4+\sin (x^2)-\ln (x)e^x+7$

คือ

$\begin{array}{cc}{f}^{\prime }(x)& =4x^{(4-1)}+\frac{d\left(x^2\right)}{dx}\cos (x^2)-\frac{d(\ln x)}{dx}{e}^x-\ln (x)\frac{d\left(e^x\right)}{dx}+0\\ & =4x^3+2x\cos (x^2)-\frac{1}{x}{e}^x-\ln (x)e^x\end{array}$

ในพจน์ที่สองของ แม่แบบ:Math คำนวณโดยใช้กฎลูกโซ่ และพจน์ที่สามใช้กฎผลคูณ นอกจากนี้ยังใช้กฎการหาอนุพันธ์สำหรับฟังก์ชันพื้นฐาน ได้แก่ x², x⁴, sin(x), ln(x) และ แม่แบบ:Nowrap รวมถึงค่าคงที่ 7 ในพจน์สุดท้าย

ดูเพิ่ม

• กณิกนันต์
• คณิตวิเคราะห์
• ปฏิยานุพันธ์
• ปริพันธ์
• ตัวผกผันการคูณ

แหล่งข้อมูลอื่น

• แม่แบบ:Springer
• Khan Academy: "Newton, Leibniz, and Usain Bolt"
• แม่แบบ:MathWorld
• Online Derivative Calculator from Wolfram Alpha.