สมการกำลังสาม

ตัวอย่างกราฟของสมการกำลังสาม

ในทางคณิตศาสตร์ สมการกำลังสาม คือสมการของพหุนามตัวแปรเดียวที่มีดีกรีเท่ากับ 3 รูปแบบทั่วไปของสมการกำลังสามคือ

$a{x}^3+b{x}^2+cx+d=0$

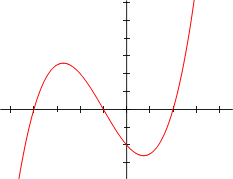
เมื่อ a ≠ 0 (ถ้า a = 0 สมการนี้จะกลายเป็นสมการกำลังสอง) โดยปกติแล้ว $a,b,c,d$ คือสัมประสิทธิ์ที่เป็นจำนวนจริง ฟังก์ชันของสมการกำลังสามสามารถวาดกราฟบนระบบพิกัดคาร์ทีเซียนได้รูปเส้นโค้งคล้ายตัว S หรือ N

ดิสคริมิแนนต์

สมการกำลังสามทุกสมการที่มีสัมประสิทธิ์เป็นจำนวนจริง จะมีรากของสมการ 3 คำตอบเสมอ ซึ่งจะต้องมีจำนวนจริงอย่างน้อยหนึ่งจำนวนที่เป็นคำตอบ ตามทฤษฎีบทค่าระหว่างกลาง (intermediate value theorem) และคำตอบเหล่านั้นอาจจะเท่ากันบางค่าก็ได้ ส่วนอีกสองจำนวนที่เหลือสามารถแยกแยะได้จากการพิจารณาดิสคริมิแนนต์ ซึ่งคำนวณจาก

$\mathrm{\Delta }=4b^{3}d-b^2{c}^2+4a{c}^3-18abcd+27a^2{d}^2$

คำตอบของสมการจะเป็นประเภทใดประเภทหนึ่ง ดังต่อไปนี้

• ถ้า Δ < 0 คำตอบของสมการจะเป็นจำนวนจริงทั้งสามค่า ที่แตกต่างกันทั้งหมด
• ถ้า Δ > 0 คำตอบของสมการจะมีหนึ่งค่าที่เป็นจำนวนจริง และอีกสองจำนวนเป็นจำนวนเชิงซ้อนสังยุคซึ่งกันและกัน
• ถ้า Δ = 0 คำตอบของสมการจะเป็นจำนวนจริงทั้งสามค่า ซึ่งมีสองจำนวนเป็นค่าเดียวกัน หรือ เป็นค่าเดียวกันทั้งสามจำนวน อย่างใดอย่างหนึ่ง

สูตรกำลังสาม

ถ้าหาก $x_1,x_2,x_3$ เป็นคำตอบของสมการกำลังสามแล้ว เราจะสามารถแยกตัวประกอบของพหุนามกำลังสามได้ดังนี้

$a{x}^3+b{x}^2+cx+d=a(x-x_1)(x-x_2)(x-x_3)=0$

กำหนดให้

$\begin{array}{cc}q& =\frac{9abc-27a^{2}d-2b^3}{54a^3}\\ r& =\sqrt{{\left(\frac{3ac-b^2}{9a^2}\right)}^3+q^2}\\ s& =\sqrt[3]{q+r}\\ t& =\sqrt[3]{q-r}\\ \end{array}$

คำตอบของสมการทั้งสามค่าสามารถคำนวณได้จากสูตร

$\begin{array}{cc}{x}_1& =s+t-\frac{b}{3a}\\ x_2& =-\frac{1}{2}(s+t)-\frac{b}{3a}+\frac{\sqrt{3}}{2}(s-t)i\\ x_3& =-\frac{1}{2}(s+t)-\frac{b}{3a}-\frac{\sqrt{3}}{2}(s-t)i\\ \end{array}$

เมื่อ i คือ หน่วยจินตภาพที่นิยามโดย i² = −1

อ้างอิง

• W. S. Anglin; & J. Lambek (1995). "Mathematics in the Renaissance", in The heritage of Thales, Ch. 24. Springers.
• Lucye Guilbeau (1930). "The History of the Solution of the Cubic Equation", Mathematics News Letter 5 (4), p. 8-12.
• R.W.D. Nickalls (1993). A new approach to solving the cubic: Cardan's solution revealed แม่แบบ:Webarchive, The Mathematical Gazette, 77:354-359.

ดูเพิ่ม

• สมการเชิงเส้น
• สมการกำลังสอง
• สมการกำลังสี่
• สมการกำลังห้า

แหล่งข้อมูลอื่น

• Tartaglia's work (and poetry) on the solution of the Cubic Equation แม่แบบ:Webarchive at Convergence แม่แบบ:Webarchive
• Cubic Equation Solver.
• Quadratic, cubic and quartic equations on MacTutor archive.
• แม่แบบ:Planetmath reference
• Cardano solution calculator as java applet แม่แบบ:Webarchive at some local site. Only takes natural coefficients.
• Graphic explorer for cubic functions With interactive animation, slider controls for coefficients
• On Solution of Cubic Equations at Holistic Numerical Methods Institute
• Dave Auckly, Solving the cubic with a pencil American Math Monthly 114:1 (2007) 29--39