ทฤษฎีระบบควบคุม

ระบบควบคุมมีความสำคัญอย่างมากในการปล่อยจรวดและยานอวกาศ

แม่แบบ:Wikibooks ทฤษฎีระบบควบคุม (แม่แบบ:Langx) เป็นสาขาหนึ่งของคณิตศาสตร์และวิศวกรรมศาสตร์ ในที่นี้ การควบคุมหมายถึง การควบคุมระบบพลศาสตร์ ให้มีค่าเอาต์พุตที่ต้องการ โดยการป้อนค่าอินพุตที่เหมาะสมให้กับระบบ ตัวอย่างที่เห็นได้ทั่วไป เช่น ระบบควบคุมอุณหภูมิห้องของเครื่องปรับอากาศ หรือ แม้แต่ลูกลอยในโถส้วม ที่เปิดน้ำปิดน้ำโดยอัตโนมัติเมื่อน้ำหมดและน้ำเต็ม

การควบคุมการขับเคลื่อนยานพาหนะ เช่น รถยนต์ ก็ถือเป็นการควบคุมชนิดหนึ่ง โดยผู้ขับขี่เป็นผู้ควบคุมทิศทางและความเร็ว ซึ่งระบบควบคุมประเภทที่ต้องมีคนเข้ามาเกี่ยวข้องนี้ถือว่าเป็น ระบบควบคุมไม่อัตโนมัติ (manual control) แต่ทฤษฎีระบบควบคุมจะครอบคลุมเฉพาะการวิเคราะห์และออกแบบ ระบบควบคุมอัตโนมัติ (automatic control) เท่านั้น เช่น ระบบขับเคลื่อนอัตโนมัติ (cruise control)

ระบบควบคุมยังอาจแบ่งออกได้เป็นระบบควบคุมวงเปิด (open-loop control) คือ ระบบควบคุมที่ไม่ได้ใช้สัญญาณจากเอาต์พุต มาบ่งชี้ถึงลักษณะการควบคุม ส่วนระบบควบคุมวงปิด (closed-loop control) หรือ ระบบป้อนกลับ (feedback control) นั้นจะใช้ค่าที่วัดจากเอาต์พุต มาคำนวณค่าการควบคุม นอกจากนี้ยังอาจแบ่งได้ตามคุณลักษณะของระบบ เช่น เป็นเชิงเส้น (linear) / ไม่เป็นเชิงเส้น (nonlinear) , แปรเปลี่ยนตามเวลา (time-varying) / ไม่เปลี่ยนแปลงตามเวลา (time-invariant) และเวลาต่อเนื่อง (Continuous time) / เวลาไม่ต่อเนื่อง (Discontinuous time)

ประวัติศาสตร์และการพัฒนาของทฤษฎีระบบควบคุม

ระบบควบคุมในยุคโบราณ

แสดงหลักการทำงานของลูกเหวี่ยงหนีศูนย์กลางที่เมื่อเครื่องจักรหมุนเร็วเกินกว่าค่าที่ต้องการลูกตุ้มจะเบนออกจากแกนกลางส่งผลให้ลิ้นควบคุมไอน้ำปล่อยไอน้ำน้อยลง ในทางกลับกันถ้าเครื่องยนต์หมุนช้าเกินไปลูกตุ้มจะหุบเข้าหาแกนกลางส่งผลให้ลิ้นควบคุมไอน้ำปล่อยไอน้ำเข้าสู่เครื่องจักรมากขึ้น

ลูกลอย (ballcock) การป้อนกลับเชิงลบรูปแบบหนึ่งที่ใช้ในการควบคุมระดับน้ำในถังเก็บน้ำ เช่น ถังเก็บน้ำบนชักโครก

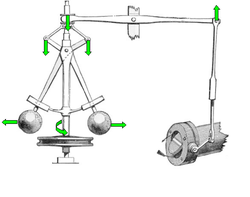
การใช้ระบบควบคุมวงปิด นั้นมีมาแต่โบราณกาล ตัวอย่างเช่น นาฬิกาน้ำของกรีก ซึ่งมีการใช้ลูกลอยในการควบคุมระดับน้ำในถัง อุปกรณ์ที่ถือว่าเป็นจุดเริ่มต้น ของการใช้ระบบควบคุมป้อนกลับในวงการอุตสาหกรรม ก็คือ ลูกเหวี่ยงหนีศูนย์กลาง (centrifugal governor หรือเรียก fly-ball governor) ในการควบคุมความเร็วในการหมุน เครื่องจักรไอน้ำที่ประดิษฐ์ขึ้นโดย เจมส์ วัตต์ ในปี ค.ศ. 1788

จุดกำเนิดของทฤษฎีระบบควบคุม

แบบจำลองคณิตศาสตร์ของระบบควบคุม

ในยุคก่อนหน้านี้ การออกแบบระบบควบคุมต่าง ๆ นั้น เป็นไปในลักษณะลองผิดลองถูก ไม่ได้มีการใช้คณิตศาสตร์ในการวิเคราะห์ ออกแบบแต่อย่างใด จนกระทั่งในปี ค.ศ. 1840 นักดาราศาสตร์ชาวอังกฤษ จอร์จ แอรี ได้ประดิษฐ์อุปกรณ์ควบคุมทิศทางของกล้องดูดาว โดยอุปกรณ์นี้จะหมุนกล้องดูดาว เพื่อชดเชยกับการหมุนของโลกโดยอัตโนมัติ ในระหว่างการออกแบบ แอรีได้สังเกตถึงความไม่เสถียร (instability) ของระบบป้อนกลับ จึงใช้สมการเชิงอนุพันธ์ในการจำลองและวิเคราะห์พฤติกรรมของระบบ การวิเคราะห์เสถียรภาพของระบบนี้เป็นหัวใจสำคัญของทฤษฎีระบบควบคุม

ทฤษฎีเสถียรภาพ

ในปี ค.ศ. 1868 เจมส์ เคลิร์ก แมกซ์เวลล์ เป็นบุคคลแรก ที่ทำการศึกษาถึงเสถียรภาพของ ลูกเหวี่ยงหนีศูนย์กลางของ เจมส์ วัตต์ โดยใช้แบบจำลองสมการเชิงอนุพันธ์เชิงเส้น ทฤษฎีเสถียรภาพของระบบเชิงเส้นของแมกซ์เวลล์นี้ พิจารณาเสถียรภาพของระบบจาก รากของสมการคุณลักษณะ (characteristic equation) ของระบบ ต่อมาในปี ค.ศ. 1892 เลียปูนอฟได้ทำการศึกษาถึงเสถียรภาพของระบบไม่เป็นเขิงเส้น และสร้างทฤษฎีเสถียรภาพของเลียปูนอฟ (Lyapunov stability) แต่ทฤษฎีของเลียปูนอฟนี้เป็นทฤษฎีที่สำคัญที่ไม่ได้รับความสนใจ จนกระทั่งหลายสิบปีต่อมา

ระบบควบคุมแบบดั้งเดิม

ระบบควบคุมแบบดั้งเดิม (แม่แบบ:Langx) หมายถึง ระบบควบคุมที่ออกแบบและวิเคราะห์บนโดเมนความถี่ (หรือโดเมนการแปลงฟูรีเย) และโดเมนการแปลงลาปลาส โดยการใช้แบบจำลองในรูปของ ฟังก์ชันส่งผ่าน (transfer function) โดยไม่ได้ใช้ข้อมูลรายละเอียดของไดนามิกส์ภายในของระบบ (internal system dynamic)

พัฒนาการของทฤษฎีระบบควบคุมในช่วงนี้นั้น ส่วนใหญ่พัฒนาขึ้นเพื่อประยุกต์ใช้งานในทางทหารและทางระบบสื่อสาร อันเนื่องมาจากสงครามโลกครั้งที่สอง และ การขยายตัวของโครงข่ายสื่อสารโทรศัพท์

พัฒนาการเพื่อใช้งานในระบบโครงข่ายโทรศัพท์

ในช่วงยุคที่มีการขยายตัวของระบบสื่อสารโทรศัพท์นั้น ระบบสื่อสารทางไกลมีความจำเป็นต้องใช้อุปกรณ์ขยายสัญญาณด้วยหลอดสุญญากาศ ในปี ค.ศ. 1927 แนวความคิดและประโยชน์ของระบบป้อนกลับแบบลบ ได้ถูกนำเสนอในรูปของ อุปกรณ์ขยายสัญญาณป้อนกลับแบบลบ (negative feedback amplifier) โดย เอช. เอส. แบล็ก แต่การวิเคราะห์เสถียรภาพของระบบขยายสัญญาณตามทฤษฎีของแมกซ์เวลล์ โดยใช้วิธีของ เราท์-ฮิวรวิทซ์ (Routh-Hurwitz) นั้นเป็นไปได้ยาก เนื่องจากความซับซ้อนของระบบ วิศวกรสื่อสารของ Bell Telephone Laboratories จึงได้นำเสนอการวิเคราะห์บนโดเมนความถี่ โดยในปี ค.ศ. 1932 แฮร์รี่ ไนควิสต์นำเสนอ เกณฑ์เสถียรภาพของไนควิสต์ (Nyquist stability criterion) ซึ่งใช้วิธีการพล็อตกราฟเชิงขั้ว ของผลตอบสนองความถี่ตลอดวงรอบ (loop frequency response) ของระบบ ต่อมาในปี ค.ศ. 1940 เฮนดริค โบดีได้นำเสนอวิธีการวิเคราะห์เสถียรภาพโดยขอบเขตอัตราขยาย (gain margin) และขอบเขตมุม (phase margin) จากกราฟระหว่างขนาดและมุม (phase) ของผลตอบสนองความถี่ เรียกว่า โบดีพล็อต (Bode plot)

พัฒนาการเพื่อการใช้งานทางด้านการทหาร

ปัญหาหลายปํญหาในทางหทาร เช่น ปัญหาการนำร่องการเดินเรืออัตโนมัติ ปัญหาการเล็งเป้าโดยอัตโนมัติ นั้นเป็นแรงผลักดันสำคัญให้เกิดการพัฒนาการทางทฤษฎีระบบควบคุมที่สำคัญหลายอย่าง ในปี ค.ศ. 1922 มินอร์สกี (N. Minorsky) ได้กำหนดและวิเคราะห์กฎของ ระบบควบคุมพีไอดี หรือ สัดส่วน-ปริพันธ์-อนุพันธ์ (proportional-integral-derivative) ซึ่งยังเป็นที่นิยมใช้อย่างกว้างขวางในปัจจุบัน เพื่อใช้ในการนำร่องการเดินเรือ ปัญหาที่สำคัญในช่วงนั้นคือ การเล็งเป้าของปืนจากเรือหรือเครื่องบิน ซึ่งในปี ค.ศ. 1934 ฮาเซน (H.L. Házen) ได้บัญญัติคำสำหรับประเภทปัญหาการควบคุมกลไกนี้ว่า กลไกเซอร์โว (servomechanisms) การวิเคราะห์และออกแบบนั้นก็ใช้วิธีการบนโดเมนความถี่ จนกระทั่งในปีค.ศ. 1948 อีแวนส์ (W. R. Evans) ซึ่งทำงานกับปัญหาทางด้านการนำร่องและควบคุมเส้นทางบิน ซึ่งส่วนใหญ่นั้นเป็นระบบที่ไม่เสถียร ได้ประสบกับปํญหาการวิเคราะห์เสถียรภาพบนโดเมนของความถี่ จึงได้หันกลับไปศึกษาถึงรากของสมการคุณลักษณะ ซึ่งเป็นวิธีการวิเคราะห์บนโดเมนการแปลงลาปลาส และได้พัฒนาวิธี ทางเดินราก (root locus) ในการออกแบบระบบ

ระบบควบคุมสมัยใหม่

แบบจำลองทางคณิตศาสตร์ของเพนดูลัมผกผันสามารถประยุกต์ใช้กับระบบควบคุมการทรงตัวของพาหนะอย่าง เซกเวย์ (Segway) ได้

อุปกรณ์ที่ต้องการความแม่นยำและความละเอียดสูงอย่างหัวอ่านข้อมูลของฮาร์ดดิสก์ จำเป็นที่จะต้องมีการออกแบบตัวควบคุมที่มีประสิทธิภาพ ทนทานต่อการรบกวนต่าง ๆ ได้เป็นอย่างดี อาทิเช่น การสั่นสะเทือน, ผลกระทบจากกระแสไฟฟ้าในระบบเกิน เป็นต้น

ระบบควบคุมสมัยใหม่ (แม่แบบ:Langx) หมายถึง ระบบควบคุมที่ไม่ได้ใช้เทคนิคในการออกแบบแบบดั้งเดิม คือ จากรากของสมการคุณลักษณะ และอยู่บนโดเมนความถี่ แต่เป็นการออกแบบ โดยมีพื้นฐานจากแบบจำลองสมการอนุพันธ์ของไดนามิกส์ของระบบ และเป็นการออกแบบอยู่บนโดเมนเวลา

แรงผลักดันของพัฒนาการจากระบบควบคุมแบบดั้งเดิม มาสู่ระบบควบคุมสมัยใหม่นี้ มีอยู่หลัก ๆ สองประการคือ

ข้อจำกัดของระบบควบคุมแบบดั้งเดิมต่องานด้านอวกาศยาน : จากความสำเร็จในการส่งดาวเทียมสปุตนิก 1 ของสหภาพโซเวียตในปี ค.ศ. 1957 นั้นกระตุ้นให้เกิดความตื่นตัวของการประยุกต์ใช้งานทางด้านอวกาศยาน ความสำเร็จของโซเวียตนั้นเนื่องมาจากพัฒนาการทางด้านทฤษฎีระบบควบคุมแบบไม่เป็นเชิงเส้น ซึ่งไม่ได้รับความสนใจมากนักจากประเทศตะวันตก เนื่องจากความล้มเหลวในการใช้เทคนิคต่าง ๆ ของระบบควบคุมแบบดั้งเดิม กับงานด้านอวกาศยาน ซึ่งระบบส่วนใหญ่นั้น เป็นระบบหลายตัวแปรแบบไม่เป็นเชิงเส้น (nonlinear multivariable system) จึงมีการหันกลับมาพิจารณาการวิเคราะห์จากปัญหาดั้งเดิม ในรูปของแบบจำลองสมการอนุพันธ์ของระบบ

การประยุกต์ใช้คอมพิวเตอร์กับงานระบบควบคุม : แม่แบบ:บทความหลัก พัฒนาการของคอมพิวเตอร์ มีส่วนสำคัญในการพัฒนาทฤษฎีต่าง ๆ ของระบบควบคุม เนื่องจากทำให้สามารถสร้างอุปกรณ์ควบคุมที่สามารถทำงานซับซ้อนได้ รวมทั้งการใช้คอมพิวเตอร์ช่วยคำนวณในการออกแบบกฎของการควบคุม ดังนั้นจึงมีการพัฒนาระบบควบคุมแบบต่าง ๆ ขึ้นอย่างมากมาย

ด้วยเหตุดังกล่าว จึงมีการพัฒนาทฤษฎีระบบควบคุม จากหลายแง่มุม

จากความพยายามในการใช้คอมพิวเตอร์ซึ่งเป็นดิจิทัล เพื่อการควบคุมระบบซึ่งโดยส่วนใหญ่จะเป็นระบบอนาล็อก จึงส่งผลให้มีการพัฒนาทางทฤษฎีระบบควบคุมดิจิทัล (แม่แบบ:Langx) โดยในปี ค.ศ. 1952 จอห์น รากัซซินี (J.R. Ragazzini) , แฟรงคลิน (G Franklin) และ ซาเดห์ (L.A. Zadeh ผู้คิดค้นฟัซซี่ลอจิก) ที่มหาวิทยาลัยโคลัมเบีย ได้พัฒนาทฤษฎีระบบแบบชักข้อมูล (sampled data systems) ขึ้น การใช้คอมพิวเตอร์ในการควบคุมกระบวนการในอุตสาหกรรมนั้น ครั้งแรกในปี ค.ศ. 1959 ที่ โรงกลั่นน้ำมัน พอร์ต อาเธอร์ (Port Arthur) ในรัฐเท็กซัส

นอกจากนั้นแล้วแนวความคิดของการควบคุมที่ซับซ้อนขึ้นโดยมีการรวม ข้อกำหนดความต้องการทางด้านประสิทธิภาพ (performance) ในการออกแบบระบบควบคุม ซึ่งเรียกว่า ระบบควบคุมแบบเหมาะสมที่สุด (optimal control) รากฐานของทฤษฎีระบบควบคุมแบบเหมาะสมที่สุดนี้มีมายาวนานตั้งแต่ปี ค.ศ. 1696 จาก หลักของความเหมาะสมที่สุด (principle of optimality) ในปัญหา บราคิสโตโครน (Brachistochrone curve) และ แคลคูลัสของการแปรผัน (Calculus of variations) ในปีค.ศ. 1957 ริชาร์ด เบลแมน ได้ประยุกต์ใช้วิธีการกำหนดการพลวัตของเขาในการแก้ปัญหาระบบควบคุมแบบเหมาะสมที่สุด แบบเวลาไม่ต่อเนื่อง ต่อมาในปีค.ศ. 1958 พอนเทรียกิน (L.S. Pontryagin) ได้พัฒนา หลักการมากที่สุด (maximum principle หรือบางครั้งก็เรียก minimum principle) สำหรับแก้ปัญหาในรูปของแคลคูลัสของการแปรผัน แบบเวลาต่อเนื่อง

ตัวกรองคาลมานนำร่อง ลูนาร์โมดูล ของ อพอลโล่ 11 สู่พื้นผิวดวงจันทร์

การสังเกตถึงผลกระทบของสัญญาณรบกวนต่อประสิทธิภาพของระบบควบคุมนั้นมีมาตั้งแต่ในช่วงระบบควบคุมยุคดั้งเดิม เช่นในช่วงสงครามโลกครั้งที่สอง ในการพัฒนาระบบควบคุมสำหรับเรดาร์ติดเครื่องบิน เพื่อควบคุมการยิง ที่ ห้องทดลองเรดิเอชัน (Radiation Lab) ที่ เอ็มไอที, ฮอลล์ (A.C. Hall) ได้ประสบปัญหาในการออกแบบ เขาได้สังเกตถึงผลกระทบจากการออกแบบที่ไม่ได้คำนึงถึงสัญญาณรบกวนต่อประสิทธิภาพของระบบ ถึงแม้ว่าจะมีการคำนึงถึงผลกระทบของสัญญาณรบกวน แต่ก็ไม่ได้มีการใช้แบบจำลองทางคณิตศาสตร์ของสัญญาณรบกวนในการวิเคราะห์แต่อย่างใด จนกระทั่ง นอร์เบิร์ต วีนเนอร์ ได้จำลองสัญญาณรบกวน โดยใช้แบบจำลองกระบวนการสตอแคสติก หรือ แบบจำลองทางสถิติ แบบเวลาต่อเนื่อง ในการพัฒนาระบบเล็งเป้าและควบคุมการยิงปืนต่อต้านอากาศยาน โดยใช้ข้อมูลจากเรดาร์ ซึ่งงานของเขาได้ถูกเก็บเป็นความลับ จนถึงปี ค.ศ. 1949 ในช่วงเดียวกันในปี ค.ศ. 1941 คอลโมโกรอฟ ก็ได้ทำการพัฒนาแบบจำลองสำหรับระบบเวลาไม่ต่อเนื่องขึ้น ระบบควบคุมที่ใช้แบบจำลองสคอแคสติกนี้ในการวิเคราะห์ จะเรียกว่า ระบบควบคุมสตอแคสติก (Stochastic control)

การวิเคราะห์และควบคุมระบบบนโดเมนเวลา โดยใช้แบบจำลองตัวแปรสถานะ หรือ แบบจำลองปริภูมิสถานะ (state space) นั้นเป็นหัวใจของทฤษฎีระบบควบคุมสมัยใหม่ รูดอล์ฟ อีมิว คาลมาน และ Bellman นั้นถือได้ว่าเป็นบุคคลที่มีส่วนสำคัญในการพัฒนาทฤษฎีระบบควบคุมโดยใช้แบบจำลองตัวแปรสถานะนี้ โดยที่ในปี ค.ศ. 1960 คาลมานได้นำทฤษฎีเสถียรภาพของเลียปูนอฟมาใช้ในการออกแบบระบบ ซึ่งเป็นผลให้ผลงานของเลียปูนอฟกลับมาได้รับความสนใจ นอกจากนี้แนวทางใหม่นี้ยังสามารถตอบคำถามเกี่ยวกับลักษณะเฉพาะของตัวระบบได้ ได้แก่ สภาพควบคุมได้ (controllability) สภาพสังเกตได้ (observability) ผลสัมฤทธิ์เล็กสุดเฉพาะกลุ่ม (minimal realization) และยังนำไปสู่การออกแบบตัวควบคุมแบบใหม่ เช่น การวางขั้ว (pole placement) ตัวควบคุมอิงตัวสังเกต (observer-based controller) และตัวควบคุมกำลังสองเชิงเส้นเหมาะที่สุด (optimal linear quadratic regulator) คาลมานได้พัฒนาวิธีการออกแบบระบบควบคุมแบบเหมาะสมที่สุด จากแบบจำลองปริภูมิสถานะ ในรูปของปัญหาระบบเชิงเส้นคงค่าแบบเหมาะสมที่สุดตามสมการกำลังสอง หรือ LQR (linear quadratic regulator) ในปีเดียวกันนี้ คาลมานได้นำเสนอผลงานของเขาในการประยุกต์ใช้แบบจำลองตัวแปรสถานะนี้เข้ากับแนวความคิดทางด้านสตอแคสติกของวีนเนอร์ และคิดค้นสิ่งที่เรารู้จักกันในชื่อ ตัวกรองคาลมาน (Kalman filter) ขึ้นมา โดยการใช้งานจริงครั้งแรกของตัวกรองคาลมาน นั้นได้ถูกประยุกต์เป็นส่วนหนึ่งของระบบนำร่องในโครงการอพอลโล ตั้งแต่นั้นมาตัวกรองคาลมานก็ได้ถูกประยุกต์ใช้งานอย่างกว้างขวางในปัจจุบัน

ในปัจจุบันแนวทางการวิเคราะห์และควบคุมระบบบนโดเมนเวลา โดยใช้แบบจำลองตัวแปรสถานะสามารถประยุกต์ใช้ได้กับงานวิศวกรรมห้วงอากาศอวกาศ (aerospace engineering) การควบคุมกระบวนการ (process control) และเศษฐมิติ (econometrics)

ประเภทของปัญหาระบบควบคุม

ปัญหาของทฤษฎีระบบควบคุมนั้น สามารถแยกออกได้เป็นประเภทใหญ่ 2 ประเภท คือ

1. ปัญหาระบบคงค่า (regulator problem) คือ ปัญหาที่มีจุดประสงค์ของการควบคุม ให้เอาต์พุตของระบบมีค่าคงที่ ต้านทานการรบกวน (disturbance) ที่เข้ามาในระบบ และมีผลทำให้ระบบเปลี่ยนแปลง
2. ปัญหาระบบปรับค่าตาม (tracking หรือ servo problem) คือ ปัญหาที่มีจุดประสงค์ของการควบคุม ให้เอาต์พุตมีค่าเท่ากับสัญญาณอ้างอิง เมื่อสัญญาณอ้างอิงเปลี่ยนไป ระบบควบคุมจะทำการปรับให้ สัญญาณเอาต์พุตมีค่าตามสัญญาณอ้างอิง

ประเภทของระบบ

เราอาจจะสามารถจำแนกประเภทของระบบได้หลายแบบตามแต่เงื่อนไขในการจำแนกระบบที่ใช้ แต่ในบริบทของทฤษฎีระบบควบคุมนั้น เรามักจำแนกระบบตามภาวะเชิงเส้น, การแปรเปลี่ยนตามเวลา และความต่อเนื่องโดเมนเวลา ดังต่อไปนี้ คือ

จำแนกตามภาวะเชิงเส้น

ระบบเชิงเส้น

ระบบเชิงเส้น (Linear Systems) คือระบบที่มีภาวะเชิงเส้น (Linearity) กล่าวคือ ถ้าให้ $x_1(t),x_2(t)$ เป็นสัญญาณขาเข้าของระบบ และ $y_i(t)=H\{x_i(t)\}$ โดยที่ $i\in \{1,2\}$เป็นสัญญาณขาออก ถ้าระบบมีภาวะเชิงเส้นแล้วจะต้องสอดคล้องกับคุณสมบัติดังนี้

$\alpha y_1(t)+\beta y_2(t)=H\{\alpha x_1(t)+\beta x_2(t)\}$

$\mathrm{\forall }\alpha ,\beta \in ℝ$

หมายเหตุ: เราเรียกหลักการข้างต้นว่าหลักการซ้อนทับ (superposition)

ระบบไม่เชิงเส้น

ระบบไม่เชิงเส้น (Nonlinear Systems) คือระบบที่ไม่มีสมบัติภาวะเชิงเส้นดังกล่าว

จำแนกตามการแปรเปลี่ยนตามเวลา

ระบบไม่แปรเปลี่ยนตามเวลา

แม่แบบ:บทความหลัก ระบบไม่แปรเปลี่ยนตามเวลา (Time-invariant system) คือระบบที่คุณสมบัติของระบบไม่เปลี่ยนไปเมื่อเวลาเปลี่ยนไป กล่าวคือ สมมุติว่าไม่มีความล่าช้าเกิดขึ้นในระบบ (ระบบรับสัญญาณขาเข้าแล้วสามารถให้สัญญาณขาออกได้ในทันที) ถ้าป้อนสัญญาณขาเข้า $x(t)$ ที่เวลา $t$ จะได้สัญญาณขาออกเป็น $y(t)$ ที่เวลา $t$ ดังนั้นหากป้อนสัญญาณขาเข้าเดิมที่เวลา $t+\delta$ นั้นคือ $x(t+\delta )$ สัญญาญาณขาออกผลลัพธ์ก็ต้องเป็น ค่าเดิม คือ $y(t+\delta )$เพียงแต่จะปรากฏที่เวลา $t+\delta$ ตามเวลาที่ป้อนสัญญาณขาเข้า $x(t+\delta )$

ระบบแปรเปลี่ยนตามเวลา

ระบบแปรเปลี่ยนตามเวลา (Time-variant system) คือระบบที่จะปลี่ยนแปลงคุณสมบัติไปตามเวลา กล่าวคือ ถ้าป้อนสัญญาณขาเข้า $x(t)$ ที่เวลา $t$ แล้วจะได้สัญญาณขาออกเป็น $y(t)$ ที่เวลา $t$ ดังนั้นหากป้อนสัญญาณขาเข้าเดิมที่เวลา $t+\delta$ นั้นคือ $x(t+\delta )$ สัญญาณขาออกผลลัพธ์ จะไม่ได้ค่าเดิม คือ $y(t+\delta )$ แต่จะเป็นค่าอื่นเพราะในช่วงเวลา $\delta$ นั้นระบบได้เปลี่ยนคุณสมบัติไปแล้ว

จำแนกตามความต่อเนื่องโดเมนเวลา

ระบบเวลาต่อเนื่อง

ระบบเวลาต่อเนื่อง (Continuous time systems) คือระบบที่มีโดเมนเวลาเป็นสมาชิกเซตของจำนวนจริง กล่าวคือ $t\in ℝ$

ระบบเวลาวิยุต

ระบบเวลาวิยุต หรือ ระบบเวลาไม่ต่อเนื่อง (Discontinuous time systems) คือระบบที่มีโดเมนเวลาเป็นสมาชิกเซตของจำนวนเต็ม (แม้ในบางครั้ง อาจจะไม่ใช้จำนวนเต็ม แต่ ถ้ากล่าวโดยไม่เสียนัยยะความเป็นทั่วไป เราสามารถแทนจำนวนเหล่านั้นที่แม้ไม่ใช้จำนวนเต็มได้ด้วย ดัชนีเวลา (time index) ที่เป็นจำนวนเต็มได้เสมอ) กล่าวคือ $t\in \mathbb{Z}$

:หมายเหตุ เรามักจะใช้อักษร $n$ หรือ $k$ แทน $t$ ในกรณีที่เป็นเวลาวิยุต

ระบบผสม

ระบบผสม (Hybrid systems) คือระบบที่โดเมนของเวลาต่อเนื่องเป็นช่วง ๆ กล่าวคือ มีทั้งช่วงที่ต่อเนื่องและไม่ต่อเนื่องในโดเมนของเวลา ตัวอย่างของระบบที่ศึกษากันคือ ระบบเชิงเส้นกระโดดแบบมาร์คอฟ (Markovian jump linear system : MJLS)

ในกรณีที่เป็น ระบบเชิงเส้นกระโดดแบบมาร์คอฟและเวลาไม่ต่อเนื่อง ระบบจะมีแบบจำลองดังต่อไปนี้

$x(k+1)=A_{r(k)}x(k)+B_{r(k)}u(k)+F_{r(k)}w(k)$

$y(k)=C_{r(k)}x(k)+G_{r(k)}v(k)$

โดยที่

$r(k)\in \{1,2,3,...m\}$ เป็นตัวแปรสถานะของกระบวนการมาร์คอฟ (Markov process) ที่มีความน่าจะเป็นในการเปลี่ยนสถานะเป็น $Prob(r(k+1)=j|r(k)=i)=q_{ij}$ และเมทริกซ์ของระบบแปรเปลี่ยนขึ้นกับ $r(k)$

$w(k)$ เป็นสัญญาณรบกวนที่มีต่อตัวระบบ

$v(k)$ เป็นสัญญาณรบกวนที่มีการสังเกต (สัญญาณขาออก)

ส่วน $x(k),y(k),A,B,C,D,F$ จะนิยามในส่วนของแบบจำลองปริภูมิสถานะ ต่อไป

ทฤษฎีระบบควบคุมแบบดั้งเดิม

ระบบควบคุมวงปิด

เนื่องจากระบบควบคุมแบบวงเปิดมีปัญหาด้านเสถียรภาพของระบบเพราะไม่มีการป้อนกลับของสัญญาณขาออก ซึ่งไม่เหมาะกับการใช้งานหลายอย่าง จึงมีความต้องการที่จะออกแบบระบบควบคุมที่สามารถตรวจจับความคลาด

เคลื่อนระหว่างสัญญาณขาออกและสัญญาณอ้างอิงได้ จึงได้มีการคิดค้นระบบควบคุมแบบป้อนกลับ (Feedback control systems) หรือระบบควบคุมแบบวงปิด (Closed loop control systems) ขึ้นมาเพื่อหลีกเลี่ยงปัญหาที่เกิด

ขึ้นกับระบบควบคุมแบบวงเปิด โดยมีโครงสร้างดังในรูป

หลักการควบคุมป้อนกลับ (Feedback control systems) เป็นหลักการพื้นฐานที่ใช้ในการควบคุมระบบพลวัตอย่างแพร่หลาย ในภาพเป็นการป้อนกลับแบบลบ (Negative feedback) เพราะสัญญาณจากเซนเซอร์ (Measured error) จะถูกนำไปหักล้างจากสัญญาณอ้างอิง (Reference input) เพื่อที่จะทำไปสร้างสัญญาณความคลาดเคลื่อน (Measured error) (ผลต่างระหว่างค่าที่ผู้ออกแบบต้องการและสัญญาณจากตัวตรวจจับ (Sensor) ) ซึ่งจะนำไปป้อนสู่ตัวควบคุม (Controller) และตัวควบคุมจะสร้างสัญญาณควบคุม (System input หรือ Control signal) ป้อนสู่ระบบพลวัต (Plant, Dynamic systems) หลังจากนั้นจะนำสัญญาณขาออกของระบบพลวัต (ที่วัดได้จากตัวตรวจจับ) มาป้อนสู่ระบบป้อนกลับต่อไปเช่นนี้เรื่อย ๆ

ระบบควบคุมแบบป้อนกลับมีความได้เปรียบเหนือกว่าระบบควบคุมแบบวงเปิด ดังต่อไปนี้

• สามารถกำจัดการรบกวนได้ (อาทิ เช่น ผลจากแรงเสียดทานที่ไม่ได้รวมอยู่ในแบบจำลองทางคณิตศาสตร์ของระบบ)
• สามารถรับประกันสมรรถนะได้มากขึ้นแม้กับแบบจำลองทางคณิตศาสตร์ที่มีตัวแปรที่มีความไม่แน่นอนอยู่ด้วย (อาทิ เช่น กรณีที่ผลจากการที่แบบจำลองทางคณิตศาสตร์ไม่สามารถอธิบายระบบได้อย่างสมบรูณแบบ)
• ระบบที่ไม่มีเสถียรภาพโดยธรรมชาติอยู่แล้วสามารถทำให้มีเสถียรภาพได้หากติดตั้งตัวควบคุมที่เหมาะสม
• ระบบมีความคงทนต่อความเปลี่ยนแปลงมากขึ้นแม้ในกรณีที่พารามิเตอร์ของระบบมีการเปลี่ยนแปลง
• ระบบสามารถปรับค่าสัญญาณขาออกตามสัญญาณอ้างอิงได้ดีมากขึ้นในปัญหาระบบปรับค่าตาม

ในบางระบบ ระบบควบคุมแบบวงปิดและวงเปิดจะใช้ควบคู่กัน โดยที่ในกรณีนี้ระบบวงเปิดจะเรียกว่า feedforward

ฟังก์ชันส่งผ่านของระบบวงปิด

A simple feedback control loop

ฟังก์ชันส่งผ่าน (transfer function) คือความสัมพันธ์ทางคณิตศาสตร์ที่ใช้แสดงถึงความสัมพันธ์ระหว่างสัญญาณขาออก (output signal) ต่อสัญญาณขาเข้า (input signal) โดยฟังก์ชันส่งผ่านสามารถหาได้จากความสัมพันธ์ดังต่อไปนี้ สมมุติให้ ตัวควบคุม $C$, ระบบพลวัต $P$, ตัวตรวจจับ $F$ เป็นเชิงเส้น และ ไม่เปลี่ยนแปลงตามเวลา (ฟังก์ชันส่งผ่านของ $C(s)$, $P(s)$, and $F(s)$ ไม่เปลี่ยนแปลงตามเวลา) และในที่นี้เราจะพิจารณาผลการแปลงการแปลงลาปลาสของฟังก์ชันส่งผ่านย่อย ๆ กล่าวคือ ฟังก์ชันส่งผ่านของ $C(s)$, $P(s)$, and $F(s)$ ซึ่งการหาฟังก์ชันส่งผ่านหาได้ดังนี้

การแปลงโดเมนเวลาเป็นโดเมนความถี่โดยใช้การแปลงลาลาส ซึ่งสัญญาณขาออกในโดเมนเวลาจะเป็นการสังวัตนาการ (Convolution) ระหว่าง สัญญาณขาเข้าและผลตอบสนองอิมพัลส์ (impulse response) เมื่อผ่านการแปลงลาลาส จะได้สัญญาณขาออกในโดเมนความถี่ ที่จะอยู่ในรูปการคูณกันระหว่าง ผลการแปลงลาลาสของผลตอบสนองอิมพัลส์ (ฟังก์ชันส่งผ่าน) และผลการแปลงลาลาสของสัญญาณขาเข้า ซึ่งทำให้การวิเคราะห์ง่ายลงไปได้มาก

$Y(s)=P(s)U(s)$

$U(s)=C(s)E(s)$

$E(s)=R(s)-F(s)Y(s).$

แก้หา $Y(s)$ ในรูปของ $R(s)$ จะได้ว่า:

$Y(s)=\left(\frac{P(s)C(s)}{1+F(s)P(s)C(s)}\right)R(s)=H(s)R(s).$

โดยที่ $H(s)=\frac{P(s)C(s)}{1+F(s)P(s)C(s)}$ เราจะเรียกว่า ฟังก์ชันส่งผ่านของระบบวงปิดของระบบ (closed-loop transfer function) แม่แบบ:Clear

ตัวควบคุมพีไอดี

ระบบควบคุมแบบสัดส่วน-ปริพันธ์-อนุพันธ์ (PID controller) เป็นระบบควบคุมแบบป้อนกลับที่ใช้กันอย่างกว้างขวาง ซึ่งค่าที่นำไปใช้ในการคำนวณเป็นค่าความผิดพลาดที่หามาจากความแตกต่างของตัวแปรในกระบวนการและค่าที่ต้องการ ตัวควบคุมจะพยายามลดค่าผิดพลาดให้เหลือน้อยที่สุดด้วยการปรับค่าสัญญาณขาเข้าของกระบวนการ ค่าตัวแปรของ PID ที่ใช้จะปรับเปลี่ยนตามธรรมชาติของระบบ

แม่แบบ:บทความหลัก ตัวควบคุมพีไอดี หรือ ตัวควบคุมแบบสัดส่วน-ปริพันธ์-อนุพันธ์ เป็นตัวควบคุมที่ได้รับความนิยมเป็นอย่างสูงและใช้งานอย่างแพร่หลาย โดยในปัจจุบันยังมีการใช้งานในแวดวงอุตสาหกรรม จนไปถึงยานอวกาศ ทั้งนี้เพราะเป็นตัวคบคุมที่มีใช้งานกันมานานและจนได้รับความไว้วางในแง่ของประสิทธิภาพ อีกทั้งแบบจำลองทางคณิตศาสตร์ของมันก็เรียบง่ายและง่ายต่อการนำไปติดตั้ง ตัวควบคุมพีไอดีมีแบบจำลองทางคณิตศาสตร์ดังต่อไปนี้

กำหนดให้ $u(t)$ คือสัญญาณควบคุมที่จะส่งให้ตัวระบบ

และ $y(t)$ คือสัญญาณขาออกที่ถูกวัดมาได้

และ $r(t)$ คือสัญญาณอ้างอิง

สัญญาณความคลาดเคลื่อนคือ $e(t)=r(t)-y(t)$ ดังนั้น

$u(t)=K_{P}e(t)+K_I\int e(t)\text{d}t+K_D\frac{\text{d}}{\text{d}t}e(t).$

สมรรถนะและเสถียรถาพของระบบจะถูกกำหนดโดยการปรับแต่งค่าพารามิเตอร์สามตัว คือ $K_P$, $K_I$ และ $K_D$ นอกเหนือจากการปรับแต่งค่าเหล่านี้หลังจากการวิเคราะห์ทางคณิตศาสตร์ของตัวระบบแล้ว ในทางปฏิบัติ ยังนิยมปรับแต่งค่าโดยใช้หลักการของ Ziegler–Nichols หรือใช้ประสบการณ์ของวิศวกร โดยที่เสถียรภาพของระบบมักขึ้นอยู่กับพารามิเตอร์ $K_P$ แต่เพียงอย่างเดียว ส่วน $K_I$ มักส่งผลในแง่ของความคงทนต่อการเปลี่ยนแปลงฉับพลันต่อตัวระบบ และ $K_D$ มักเกี่ยวกับรูปร่างของผลตอบสนอง เมื่อพิจารณาบนโดเมนการแปลงลาปลาส จะได้ว่า

$u(s)=K_{P}e(s)+K_I\frac{1}{s}e(s)+K_{D}se(s)$

$u(s)=(K_P+K_I\frac{1}{s}+K_{D}s)e(s)$

โดยจะเห็นได้ว่าฟังกชั่นส่งผ่านของตัวควบคุมพีไอดีคือ

$C(s)=(K_P+K_I\frac{1}{s}+K_{D}s).$

แม้ระบบควบคุมแบบดั้งเดิมที่ใช้ตัวควบคุมพีไอดีจะมีความสามารถที่ถูกปรับปรุงดีขึ้นมากกว่าระบบควบคุมแบบเปิดมาก แต่ก็ยังเหมาะแค่กับระบบที่มีสัญญาณเข้าทางเดียวและสัญญาณขาออกทางเดียว (Single-Input and Single-Output or SISO) และยังไม่สามารถใช้ควบคุมระบบที่มีความซับซ้อนสูงได้ โดยเฉพาะอย่างยิ่งระบบที่มีสัญญาณขาเข้าหลายทางและสัญญาณขาออกหลายทาง (Multiple-Input and Multiple-Output or MIMO)

ทฤษฎีระบบควบคุมสมัยใหม่

ระบบพลวัตส่วนใหญ่มักมีพฤติกรรมที่สามารถใช้สมการอนุพันธ์อันดับใด ๆ มาอธิบายได้ ในขณะเดียวกันสมการเชิงอนุพันธ์อันดับใด ๆ ก็สามารถลดอันดับให้เหลือเพียงสมการเชิงอนุพันธ์อันดับหนึ่งได้ จากความจริงตรงนี้จึงได้มีการเสนอวิธีการใหม่ในการวิเคราะห์และควบคุมระบบ ซึ่งจะวิเคราะห์บนโดเมนเวลาและได้มีการนำแบบจำลองปริภูมิสถานะ (state space) มาใช้ซึ่งจะอยู่ในรูปของสมการอนุพันธ์อันดับหนึ่งและแตกต่างจากระบบควบคุมแบบดั้งเดิมที่นิยมวิเคราะห์พฤติกรรมของระบบบนโดเมนความถี่ นอกจากนี้การนำแบบจำลองปริภูมิสถานะมาใช้ทำให้เราสามารถสร้างแบบจำลองทางคณิตศาสตร์สำหรับระบบแบบสัญญาณขาเข้าหลายทางสัญญาณขาออกหลายทาง (MIMO) ได้โดยการกำหนดมิติของตัวแปรในสมการปริภูมิสถานะอย่างเหมาะสม

แบบจำลองปริภูมิสถานะ(state space)

กรณีระบบเชิงเส้น

กำหนดให้ระบบพลวัตมี $p$ สัญญาณขาเข้า $q$ สัญญาณขาออก และ $n$ ตัวแปรสถานะ

สมการปริภูมิสถานะคือ:

$\dot{𝐱}(t)=A(t)𝐱(t)+B(t)𝐮(t)$

$𝐲(t)=C(t)𝐱(t)+D(t)𝐮(t)$

โดยที่:

$𝐱(\cdot )$ คือ เวกเตอร์ของตัวแปรสถานะ (state vector) ,   $𝐱(t)\in {ℝ}^n$;

$𝐲(\cdot )$ คือ เวกเตอร์ของสัญญาณขาออก (output vector) ,   $𝐲(t)\in {ℝ}^q$;

$𝐮(\cdot )$ คือ เวกเตอร์ของสัญญาณขาเข้า หรือ เวกเตอร์ของสัญญาณควบคุม (input vector, control vector) ,   $𝐮(t)\in {ℝ}^p$;

$A(\cdot )$ คือ เมทริกซ์ของตัวแปรสถานะ หรือ เมทริกซ์พลวัต (state matrix, dynamics matrix) ,   $\dim [A(\cdot )]=n\times n$,

$B(\cdot )$ คือ เมทริกซ์ขาเข้า (input matrix) ,   $\dim [B(\cdot )]=n\times p$,

$C(\cdot )$ คือ เมทริกซ์ขาออก (output matrix) ,   $\dim [C(\cdot )]=q\times n$,

$D(\cdot )$ คือ เมทริกซ์ป้อนผ่าน (feedthrough (or feedforward) matrix) (ในกรณีที่ระบบไม่มีการป้อนสัญญาณขาเข้า, $D(\cdot )$ เป็นเมทริกซ์ศูนย์),   $\dim [D(\cdot )]=q\times p$,

$\dot{𝐱}(t):=\frac{\mathrm{d}}{\mathrm{d}t}𝐱(t)$.

โดยทั่วไปแล้ว เมทริกซ์ข้างต้นจะเป็นเมทริกซ์แปรผันตามเวลาได้ แต่ในกรณีเฉพาะที่ระบบไม่แปรผันตามเวลา (LTI) มักจะถูกนำมาศึกษาอยางแพร่หลายเพราะมีความซับซ้อนน้อยกว่าและเหมาะต่อการศึกษาในระดับพื้นฐาน นอกจากนี้ตัวแปรเวลาสามารถมีได้ทั้งแบบเวลาต่อเนื่อง (continuous time : $t\in ℝ$) และแบบเวลาวิยุต (ไม่ต่อเนื่อง) (discrete time : $t\in \mathbb{Z}$) โดยในกรณีของเวลาไม่ต่อเนื่องมักนิยมใช้ตัวแปร $k$ นอกเหนื่อจากระบบแบบที่กล่าวมาแล้วยังมีระบบผสมซึ่งเป็นระบบที่มีโดเมนของเวลาอยู่ทั้งบนแกนเวลาต่อเนื่องและไม่ต่อเนื่อง

สมการปริภูมิสถานะ(state space equation)ข้างต้นหากพิจารณาตามโดเมนของเวลาจะมีรูปแบบต่าง ๆ กันดังต่อไปนี้ :

ชนิดของระบบ	แบบจำลองสมการปริภูมิสถานะ
เวลาต่อเนื่องและไม่เปลี่ยนแปรตามเวลา (Continuous time-invariant)	$\dot{𝐱}(t)=A𝐱(t)+B𝐮(t)$ $𝐲(t)=C𝐱(t)+D𝐮(t)$
เวลาต่อเนื่องและเปลี่ยนแปรตามเวลา (Continuous time-variant)	$\dot{𝐱}(t)=𝐀(t)𝐱(t)+𝐁(t)𝐮(t)$ $𝐲(t)=𝐂(t)𝐱(t)+𝐃(t)𝐮(t)$
เวลาไม่ต่อเนื่องและไม่เปลี่ยนแปรตามเวลา (Explicit discrete time-invariant)	$𝐱(k+1)=A𝐱(k)+B𝐮(k)$ $𝐲(k)=C𝐱(k)+D𝐮(k)$
เวลาไม่ต่อเนื่องและเปลี่ยนแปรตามเวลา (Explicit discrete time-variant)	$𝐱(k+1)=𝐀(k)𝐱(k)+𝐁(k)𝐮(k)$ $𝐲(k)=𝐂(k)𝐱(k)+𝐃(k)𝐮(k)$
โดเมนการแปลงการแปลงลาปลาส โดยที่เวลาต่อเนื่องและไม่เปลี่ยนแปรตามเวลา (Laplace domain of continuous time-invariant)	$s𝐗(s)=A𝐗(s)+B𝐔(s)$ $𝐘(s)=C𝐗(s)+D𝐔(s)$
โดเมน Z โดยที่เวลาไม่ต่อเนื่องและไม่เปลี่ยนแปรตามเวลา (Z-domain of discrete time-invariant)	$z𝐗(z)=A𝐗(z)+B𝐔(z)$ $𝐘(z)=C𝐗(z)+D𝐔(z)$

กรณีระบบไม่เชิงเส้น

$\dot{𝐱}(t)=𝐟(t,x(t),u(t))$

$𝐲(t)=𝐡(t,x(t),u(t))$

สภาพควบคุมได้

แม่แบบ:บทความหลัก สภาพควบคุมได้ (แม่แบบ:Langx) จะบ่งบอกถึงความสามารถที่สัญญาณขาเข้าที่เป็นไปได้ (admissible inputs) จะสามารถขับเคลื่อนตัวแปรสถานะให้ไปถึงค่าใด ๆ ได้ในช่วงเวลาจำกัด (เวลาอันตะ) ไม่ว่าค่าเริ่มต้น (initial value) ของตัวแปรสถานะนั้น ๆ จะเป็นค่าอะไร ในกรณีระบบพลวัตเชิงเส้นเวลาต่อเนื่องไม่แปรผันตามเวลานั้นเงื่อนไขที่จะทำให้มีสภาพควบคุมได้ ก็ต่อเมื่อ

$\mathrm{rank}\left[\begin{array}{ccccc}B& AB& A^{2}B& ...& A^{n-1}B\end{array}\right]=n$

หมายเหตุ : ค่าลำดับขั้น (Rank) คือ ค่าซึ่งแสดงถึงจำนวนแถว (หรือหลัก) ในเมทริกซ์ที่มีความอิสระเชิงเส้น (linearly independent) ต่อกัน

สภาพสังเกตได้

สภาพสังเกตได้ (แม่แบบ:Langx) เป็นสภาพที่บ่งบอกว่าระบบพลวัตมีความสามารถที่จะส่งผ่านข้อมูลของตัวแปรสถานะได้ดีแค่ไหนเมื่อพิจารณาจากสัญญาณขาออก สภาพควบคุมได้ และ สภาพสังเกตได้ เป็นสภาพคู่กันทางคณิตศาสตร์ (Duality) กล่าวคือ ในขณะที่ สภาพควบคุมได้ หมายถึง สภาพที่แสดงออกว่าสัญญาณขาเข้าสามารถขับเคลื่อนตัวแปรสถานะไปที่ค่าใด ๆ ที่ต้องการได้ แต่ สภาพสังเกตได้ จะเป็นสภาพที่แสดงออกถึงสัญญาณขาออก (output trajectory) จะให้ข้อมูลเพียงพอต่อการคาดคะเนค่าเริ่มต้นของตัวแปรสถานะของระบบได้ ในกรณีระบบพลวัตเชิงเส้นเวลาต่อเนื่องไม่แปรผันตามเวลานั้น เงื่อนไขที่จะทำให้มีสภาพสังเกตได้ได้ ก็ต่อเมื่อ

$\mathrm{rank}\left[\begin{array}{c}C\\ CA\\ ...\\ C{A}^{n-1}\end{array}\right]=n$

การแยกตัวประกอบคาลมาน

แม่แบบ:บทความหลัก การแยกตัวประกอบคาลมาน (แม่แบบ:Langx) เป็นกระบวนการแยกส่วนประกอบของเมทริกซ์ในสมการปริภูมิสถานะของระบบเชิงเส้นไม่เปลี่ยนตามเวลา linear time-invariant (LTI) ให้อยู่ในรูปแบบที่สามารถจำแนกได้ว่าส่วนใดในเมทริกซ์ของระบบ มีผลต่อ สภาพสังเกตได้ และสภาพควบคุมได้ ทำให้ง่ายต่อการวิเคราะห์คุณลักษณะของระบบ

จากสมการปริภูมิสถานะของระบบข้างต้น จะเห็นได้ว่าพารามิเตอร์ที่กำหนดลักษณะของระบบ LTI สามารถเขียนโดยย่อได้เป็นเวกเตอร์ $(A,B,C,D)$ ในที่นี้จะสมมุติว่าระบบมีมิติเป็น $n$.

การแยกตัวประกอบคาลมาน ถูกนิยามว่า คือ การแปลงเวกเตอร์ $(A,B,C,D)$ ให้เป็น $(\hat{A},\hat{B},\hat{C},\hat{D})$ โดยคูณเมทริกซ์การแปลง $T$ ดังต่อไปนี้

$\hat{A}=T^{-1}AT$

$\hat{B}=T^{-1}B$

$\hat{C}=CT$

$\hat{D}=D$

โดยเมทริกซ์การแปลง $T$ มีมิติ $n\times n$ เป็นเมทริกซ์ผกผันได้ ถูกนิยามดังต่อไปนี้ ดังต่อไปนี้:

$T=\left[\begin{array}{cccc}{T}_{r\bar{o}}& T_{ro}& T_{\overline{ro}}& T_{\bar{r}o}\end{array}\right]$

โดยที่

• $T_{r\bar{o}}$ เป็นเมทริกซ์ที่หลัก span ปริภูมิย่อย ของตัวแปรสถานะที่มีสถาพเข้าถึงได้ (reachable) และ ไม่มีสภาพสังเกตได้ (unobservable)
• $T_{ro}$ ถูกเลือกโดยที่หลักของ $\left[\begin{array}{cc}{T}_{r\bar{o}}& T_{ro}\end{array}\right]$ เป็นฐานหลักของปริภูมิย่อยที่มีสภาพเข้าถึงได้ (reachable)
• $T_{\overline{ro}}$ ถูกเลือกโดยที่หลักของ $\left[\begin{array}{cc}{T}_{r\bar{o}}& T_{\overline{ro}}\end{array}\right]$ เป็นฐานหลักของปริภูมิย่อยที่ไม่มีสภาพสังเกตได้ (unobservable)
• $T_{\bar{r}o}$ ถูกเลือกโดยที่ $\left[\begin{array}{cccc}{T}_{r\bar{o}}& T_{ro}& T_{\overline{ro}}& T_{\bar{r}o}\end{array}\right]$ ยังสามารถผกผันได้

จะเห็นได้ว่าโดยการสร้งเมทริกซ์ $T$ ในลักษณะข้างต้น เมทริกซ์ $T$ จึงผกผันได้ เป็นที่น่าสังเกตว่าเมทริกซ์ย่อยในเมทริกซ์ $T$ นั้นสามารถเป็นเมทริกซ์ศูนย์ได้ ยกตัวอย่างเช่น กรณีที่ระบบมีสภาพสังเกตได้และควบคุมได้ เมทริกซ์ $T$ ลดรูปเหลือ $T=T_{ro}$ โดยที่ เมทริกซ์ย่อยอื่นเป็นเมทริกซ์ศูนย์

รูปแบบมาตรฐาน

ระบบที่ได้รับการแปลงแล้ว $(\hat{A},\hat{B},\hat{C},\hat{D})$ จะมีรูปแบบดังต่อไปนี้:

$\hat{A}=\left[\begin{array}{cccc}{A}_{r\bar{o}}& A_{12}& A_{13}& A_{14}\\ 0& A_{ro}& 0& A_{24}\\ 0& 0& A_{\overline{ro}}& A_{34}\\ 0& 0& 0& A_{\bar{r}o}\end{array}\right]$

$\hat{B}=\left[\begin{array}{c}{B}_{r\bar{o}}\\ B_{ro}\\ 0\\ 0\end{array}\right]$

$\hat{C}=\left[\begin{array}{cccc}0& C_{ro}& 0& C_{\bar{r}o}\end{array}\right]$

$\hat{D}=D$

โดยที่

• ระบบย่อย $(A_{ro},B_{ro},C_{ro},D)$ มี สภาพเข้าถึงได้ และ สภาพสังเกตได้
• ระบบย่อย $(\left[\begin{array}{cc}{A}_{r\bar{o}}& A_{12}\\ 0& A_{ro}\end{array}\right],\left[\begin{array}{c}{B}_{r\bar{o}}\\ B_{ro}\end{array}\right],\left[\begin{array}{cc}0& C_{ro}\end{array}\right],D)$ มี สภาพเข้าถึงได้
• ระบบย่อย $(\left[\begin{array}{cc}{A}_{ro}& A_{24}\\ 0& A_{\bar{r}o}\end{array}\right],\left[\begin{array}{c}{B}_{ro}\\ 0\end{array}\right],\left[\begin{array}{cc}{C}_{ro}& C_{\bar{r}o}\end{array}\right],D)$ มี สภาพสังเกตได้

บุคคลสำคัญในวงการทฤษฎีระบบควบคุม

• อเล็กซานเดอร์ มิคาอิลโลวิช เลียปูนอฟ (ค.ศ. 1857 – ค.ศ. 1918) ในคริสต์ทศวรรษ 1890 นำเสนอเรื่องทฤษฎีเสถียรภาพของเลียปูนอฟ (Lyapunov stability) ซึ่งใช้วิเคราะห์ได้ทั้งระบบเชิงเส้นและไม่เชิงเส้นและเป็นทฤษฎีเสถียรภาพหลักในแขนงวิชาระบบควบคุมที่ยังใช้กันจนถึงถูกวันนี้
• แฮโรลด์ สตีเฟน แบล็ก (ค.ศ. 1898 – ค.ศ. 1983), นำเสนอแนวคิดเรื่องการป้อนกลับแบบลบ (negative feedback amplifiers) ในปี ค.ศ. 1927 และพัฒนาตัวขยายสัญญาณป้อนกลับแบบลบที่เสถียร์ได้สำเร็จในคริสต์ทศวรรษ 1930
• แฮร์รี่ ไนควิสต์ (ค.ศ. 1889 – ค.ศ. 1976) นำเสนอเกณฑ์เสถียรภาพของไนควิสต์ (Nyquist stability criterion) ในปี ค.ศ. 1932
• ริชาร์ด เบลแมน (Richard Bellman) (ค.ศ. 1920 – ค.ศ. 1984) ได้ประยุกต์ใช้วิธีการ กำหนดการพลวัตของเขา ในการแก้ปัญหาระบบควบคุมแบบเหมาะสมที่สุด แบบเวลาไม่ต่อเนื่อง ในปี ค.ศ. 1957
• อันเดรย์ คอลโมโกรอฟ (ค.ศ. 1903 – ค.ศ. 1987) พัฒนา Wiener-Kolmogorov filter ในปี ค.ศ. 1941 (ช่วงเวลาเดียวกับนอร์เบิร์ต วีนเนอร์)
• นอร์เบิร์ต วีนเนอร์ (Norbert Wiener) (ค.ศ. 1894 – ค.ศ. 1964) พัฒนา Wiener-Kolmogorov filter และนำเสนอศัพท์คำว่า cybernetics ในคริสต์ทศวรรษ 1940
• จอห์น อาร์ รากัซซินี (ค.ศ. 1912 – ค.ศ. 1988) นำเสนอระบบควบคุมแบบดิจิทัล และการแปลง z (z-transform) ในคริสต์ทศวรรษ 1950
• เลฟ พอนเทรียกิน (L.S. Pontryagin) (ค.ศ. 1908 – ค.ศ. 1988) หลักการมากที่สุด (maximum principle หรือบางครั้งก็เรียก minimum principle) สำหรับแก้ปัญหาในรูปของแคลคูลัสของการแปรผัน แบบเวลาต่อเนื่อง หลักการ แบง-แบง (bang-bang principle)
• รูดอล์ฟ อีมิว คาลมาน (ค.ศ. 1930 – ปัจจุบัน) ผู้พัฒนาตัวกรองคานมานและเป็นผู้นำเสนอแบบจำลองปริภูมิสถานะ และนำเสนอแนวคิดเรื่องสภาพควบคุมได้และสภาพสังเกตได้ มาใช้ในการสร้างแบบจำลองทางคณิตศาสตร์ของระบบ อันเป็นการนำองค์ความรู้ของทฤษฎีระบบควบคุมไปสู่ยุคใหม่ ที่เรียกว่า ทฤษฎีระบบควบคุมสมัยใหม่

สาขาของทฤษฎีระบบควบคุม

• ระบบควบคุมเชิงเส้น (linear control systems)
• ระบบควบคุมไม่เป็นเชิงเส้น (nonlinear control systems)
• ระบบควบคุมดิจิทัล (digital control systems)
• ระบบควบคุมแบบเหมาะสมที่สุด (optimal control systems)
• ระบบควบคุมสตอแคสติค (stochastic control systems)
• ระบบควบคุมแบบคงทน (robust control systems)
• ระบบควบคุมแบบปรับตัวได้ (adaptive control systems)
• ระบบควบคุมแบบชาญฉลาด (intelligent control systems)

ดูเพิ่ม

ตัวอย่างการประยุกต์ทฤษฎีระบบควบคุม

• Automation
• Deadbeat Controller
• Distributed parameter systems
• Fractional order control
• H-infinity loop-shaping
• Hierarchical control system
• Model predictive control
• Process control
• Robust control
• Servomechanism
• แบบจำลองปริภูมิสถานะ
• เพนดูลัมผกผัน (Inverted pendulum)
• เพนดูลัมผกผันแบบฟูรุตะ (Furuta pendulum)
• หุ่นยนต์
• อาซิโม
• คิวริโอ
• วิทยาการหุ่นยนต์
• หุ่นยนต์ฮิวแมนนอยด์
• เมคคาทรอนิกส์

หัวข้อที่น่าสนใจในทฤษฎีระบบควบคุม

• Dual control theory
• การประมาณค่าตัวแปรสถานะ
• Filtering problem (stochastic processes)
• linear-quadratic-Gaussian (LQG) control problem
• Coefficient diagram method
• Control reconfiguration
• Feedback
• H infinity
• Hankel singular value
• Krener's theorem
• Lead-lag compensator
• Minor loop feedback
• Radial basis function
• Root locus
• Signal-flow graphs
• Stable polynomial
• Underactuation
• ระบบควบคุมพีไอดี
• การแปลงลาปลาส
• การแปลง Z ขั้นสูง
• ฟังก์ชันเลียปูนอฟ
• สมการเลียปูนอฟ
• การป้อนกลับสถานะแบบเต็ม
• ดับเบิล อินทิเกรตเตอร์

ดูเพิ่มเติม

• Automation and Remote Control
• Bond graph
• Control engineering
• Controller (control theory)
• Cybernetics
• Perceptual Control Theory
• Intelligent control
• Mathematical system theory
• Systems theory
• People in systems and control
• Time scale calculus
• Negative feedback amplifier
• Control-Feedback-Abort Loop

แหล่งข้อมูลอื่น

• สื่อการสอนเกี่ยวกับทฤษฎีระบบควบคุม แม่แบบ:Webarchive ของ มหาวิทยาลัยคาร์เนกีเมลลอน
• หนังสือ Robust Adaptive Control แม่แบบ:Webarchive โดย Petros A. Ioannou
• Franklin, G.F., Powel, J.D., and Emami-Naeini, A. Feedback Control of Dynamic Systems, 4^thed., Prentice Hall 2002 แม่แบบ:Webarchive
• Aström, K.J. Control System Design chap.1 preprint 2002
• Lewis, F.L. Applied Optimal Control and Estimation Prentice Hall 1992
• Bellman, R. "Eye of The Hurricane: an autobiography" World Scientific Publishing Co Pte Ltd. 1984
• A New Approach to Linear Filtering and Prediction Problems, by R. E. Kalman, 1960
• Katsuhiko Ogata, Modern control engineering (Edition 5), Prentice Hall, 2010, ISBN 0136156738,9780136156734
• M.W. Spong and M. Vidyasagar. Dynamics and Control of Root Manipulators. John Wiley, 1989
• เดวิด บรรเจิดพงศ์ชัย, ภาควิชาวิศวกรรมไฟฟ้า คณะวิศวกรรมศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย "ระบบควบคุมพลวัต การวิเคราะห์ การออกแบบ และการประยุกต์ (Dynamical Control Systems Analysis, Design and Applications) " สำนักพิมพ์แห่งจุฬาลงกรณ์มหาวิทยาลัย 2551 (ISBN 978-974-03-2205-4)
• วิบูลย์ แสงวีระพันธุ์ศิริ, ภาควิชาวิศวกรรมเครื่องกล คณะวิศวกรรมศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย "การควบคุมระบบพลศาสตร์ (Control of Dynamic Systems) " สำนักพิมพ์แห่งจุฬาลงกรณ์มหาวิทยาลัย 2548 (ISBN 974-13-3393-5)
• Kansas State University Control Lab แม่แบบ:Webarchive
• MIT Lecture Note on Dynamic Systems and Control by Munther Dahleh, Mohammed Dahleh, and George Verghese แม่แบบ:Webarchive