ทฤษฎีบทค่ามัชฌิม

{{#invoke:sidebar|collapsible | class = plainlist | titlestyle = padding-bottom:0.25em; | pretitle = บทความนี้เป็นส่วนหนึ่งของ | title = แคลคูลัส | image = $\underset{a}{\overset{b}{\int }}{f}^{\prime }(t)dt=f(b)-f(a)$ | listtitlestyle = text-align:center; | liststyle = border-top:1px solid #aaa;padding-top:0.15em;border-bottom:1px solid #aaa; | expanded =

| abovestyle = padding:0.15em 0.25em 0.3em;font-weight:normal; | above = ทฤษฎีบทมูลฐาน แม่แบบ:Startflatlist

• ลิมิตของฟังก์ชัน
• ความต่อเนื่อง

• ทฤษฎีบทค่าเฉลี่ย
• ทฤษฎีบทของโรลล์

| list2name = อนุพันธ์ | list2titlestyle = display:block;margin-top:0.65em; | list2title = แคลคูลัสเชิงอนุพันธ์ | list2 =

แม่แบบ:Sidebar

| list3name = ปริพันธ์ | list3title = แคลคูลัสเชิงปริพันธ์ | list3 =

แม่แบบ:Sidebar

| list4name = อนุกรม | list4title = อนุกรม | list4 =

แม่แบบ:Sidebar

| list5name = เวกเตอร์ | list5title = แคลคูลัสเวกเตอร์ | list5 =

แม่แบบ:Sidebar

| list6name = หลายตัวแปร | list6title = แคลคูลัสหลายตัวแปร | list6 =

แม่แบบ:Sidebar

| list7name = พิเศษ | list7title = พิเศษ | list7 = แม่แบบ:Startflatlist

• แคลคูลัสเชิงเศษส่วน
• มาลียาแว็ง
• แคลคูลัสเฟ้นสุ่ม
• แคลคูลัสของการแปรผัน

}}

ฟังก์ชันต่อเนื่องบนช่วง [a, b] และหาอนุพันธ์ได้บนช่วง (a, b) จะมี c ที่อยู่ในช่วง (a, b) ซึ่งเส้นที่เชื่อมระหว่างจุดปลายของช่วง [a, b] จะขนานกับเส้นสัมผัสจุด c

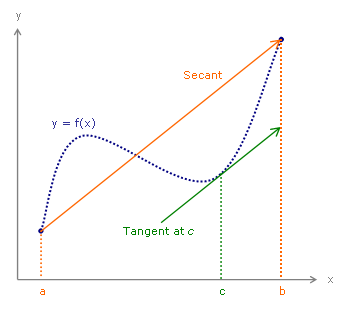
ทฤษฎีบทค่ามัชฌิม หรือ ทฤษฎีบทค่าเฉลี่ย (แม่แบบ:Langx) เป็นทฤษฎีบทในแคลคูลัสและการวิเคราะห์เชิงจริง ซึ่งกล่าวว่า สำหรับส่วนของเส้นโค้งใด ๆ ที่กำหนดให้ จะมีจุดหนึ่งจุดอยู่บนส่วนของเส้นโค้ง ที่เส้นสัมผัส ณ จุดนั้นจะขนานกับเส้นเชื่อมจุดปลายทั้งสองข้างของเส้นโค้ง

ทฤษฎีบทค่ามัชฌิมเป็นรูปนัยทั่วไปของทฤษฎีบทของโรลล์ แม่แบบ:Clear

ทฤษฎีบทค่ามัชฌิมของโคชี

รูปแบบด้านล่างเป็นนัยทั่วไปหนึ่งของทฤษฎีบทค่ามัชฌิม ซึ่งรู้จักกันในชื่อ ทฤษฎีบทค่ามัชฌิมของโคชี (Cauchy's mean value theorem) หรือ ทฤษฎีบทค่ามัชฌิมแบบขยาย (extended mean value theorem)แม่แบบ:ทฤษฎีบทคณิตศาสตร์