กฎของโคไซน์

รูปที่ 1 – กำหนดรูปสามเหลี่ยม มุม แม่แบบ:Math (หรือ แม่แบบ:Math), แม่แบบ:Math (หรือ แม่แบบ:Math), และ แม่แบบ:Math (หรือ แม่แบบ:Math) เป็นมุมตรงข้ามด้าน แม่แบบ:Math, แม่แบบ:Math, และ แม่แบบ:Math

แม่แบบ:ตรีโกณมิติ ในตรีโกณมิติ กฎของโคไซน์ (แม่แบบ:Langx) เป็นกฎที่เกี่ยวกับความสัมพันธ์ระหว่างความยาวด้านของรูปสามเหลี่ยมกับโคไซน์ของมุมหนึ่งในรูปสามเหลี่ยมนั้น กฎของโคไซน์เขียนได้ดังสมการต่อไปนี้ กำหนดให้ชื่อของด้านและมุมเป็นไปตามรูปที่ 1

$c^2=a^2+b^2-2ab\cos \gamma$

เมื่อ แม่แบบ:Math เป็นมุมระหว่างด้านที่มีความยาว แม่แบบ:Math และ แม่แบบ:Math และตรงข้ามกับด้านที่มีความยาว แม่แบบ:Math

กฎของโคไซน์นั้นกล่าวครอบคลุมถึงทฤษฎีบทพีทาโกรัสด้วย ซึ่งเป็นทฤษฎีบทสำหรับรูปสามเหลี่ยมมุมฉากเท่านั้น ถ้ามุม แม่แบบ:Math เป็นมุมฉาก (มีขนาด 90° หรือ แม่แบบ:Sfrac เรเดียน) แล้ว แม่แบบ:Math จะได้กฎของโคไซน์ที่ลดรูปเป็นทฤษฎีบทพีทาโกรัส

$c^2=a^2+b^2$

กฎของโคไซน์มีประโยชน์ในการคำนวณความยาวด้านที่สามของรูปสามเหลี่ยม เมื่อทราบความยาวด้านสองด้านและมุมที่มีด้านทั้งสองนั้นเป็นด้านประกอบ และสามารถคำนวณมุมของรูปสามเหลี่ยมได้ ถ้าทราบความยาวด้านทั้งสาม

การพิสูจน์

การใช้สูตรระยะทางระหว่างจุดสองจุด

รูปที่ 2 – การพิสูจน์โดยใช้พิกัดทางเรขาคณิต

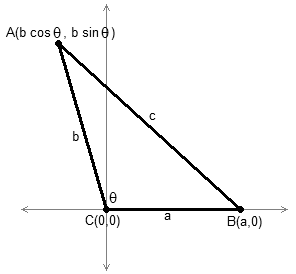
พิจารณารูปสามเหลี่ยมที่มีด้านยาว แม่แบบ:Math, แม่แบบ:Math, แม่แบบ:Math, เมื่อ แม่แบบ:Math คือ ขนาดของมุมตรงข้ามของด้านยาว แม่แบบ:Math รูปสามเหลี่ยมรูปนี้สามารถวางบนระบบพิกัดคาร์ทีเชียนโดยการลงจุดดังรูปที่ 2

$A=(b\cos \theta ,b\sin \theta ),B=(a,0),\text{and}C=(0,0)$

จากสูตรระยะทางระหว่างจุดสองจุด จะได้

$c=\sqrt{(a-b\cos \theta {)}^2+(0-b\sin \theta {)}^2}$

จากนั้นแก้สมการ

$\begin{array}{cc}{c}^2& =(a-b\cos \theta {)}^2+(-b\sin \theta {)}^2\\ c^2& =a^2-2ab\cos \theta +b^2{\cos }^2\theta +b^2{\sin }^2\theta \\ c^2& =a^2+b^2({\sin }^2\theta +{\cos }^2\theta )-2ab\cos \theta \\ c^2& =a^2+b^2-2ab\cos \theta \end{array}$

ข้อดีของการพิสูจน์นี้ คือ มันไม่จำเป็นต้องพิจารณาแยกเป็นกรณีต่าง ๆ ว่าเป็นรูปสามเหลี่ยมมุมแหลม มุมฉาก หรือมุมป้าน

การใช้ทฤษฎีบทพีทาโกรัส

ลากเส้นตรง $AD$ ให้ตั้งฉากกับ $BC$

สมมติให้ $DC$ ยาว $x$ หน่วย

จาก $\cos \gamma =\frac{x}{b}$ ดังนั้น $x=b\cos \gamma$

โดยทฤษฎีบทของปีทากอรัส เราได้ว่า

$c^2-(a-x{)}^2=b^2-x^2$

$c^2-a^2+2ax-x^2=b^2-x^2$

$c^2=a^2+b^2-2ax$

เนื่องจาก $x=b\cos \gamma$

$\therefore c^2=a^2+b^2-2ab\cos \gamma$

นอกจากนี้เรายังได้ความสัมพันธ์

$a^2=b^2+c^2-2bc\cos \alpha$

$b^2=a^2+c^2-2ac\cos \beta$

ซึ่งสามารถพิสูจน์ได้ในทำนองเดียวกัน

ดูเพิ่ม

• กฎของไซน์
• กฎของแทนเจนต์
• กฎของโคแทนเจนต์
• รายการเอกลักษณ์ตรีโกณมิติ

แหล่งข้อมูลอื่น

• แม่แบบ:Springer
• Several derivations of the Cosine Law, including Euclid's at cut-the-knot
• Interactive applet of Law of Cosines