การจับกลุ่มข้อมูลแบบค่าเฉลี่ย k

แม่แบบ:Machine learning bar การจับกลุ่มข้อมูลแบบค่าเฉลี่ย k (แม่แบบ:Langx) เป็นวิธีหนึ่งในวิธีการแบ่งเวกเตอร์ที่มีรากฐานมาจากการประมวลผลสัญญาณ วิธีนี้เป็นที่นิยมสำหรับการจับกลุ่มข้อมูลในการทำเหมืองข้อมูล การจับกลุ่มข้อมูลแบบค่าเฉลี่ย k ใช้สำหรับการแบ่งการสังเกตจำนวน n สิ่งเป็น k กลุ่ม โดยแต่ละการสังเกตจะอยู่ในกลุ่มที่มีค่าเฉลี่ย(ที่ใช้เป็นแม่แบบ)ใกล้เคียงกันที่สุด โดยวิธีนี้จะเป็นการแบ่งพื้นที่ข้อมูลไปเป็นแผนภาพโวโรนอย

วิธีการจัดกลุ่มนี้อยู่ในกลุ่มความซับซ้อนของปัญหาเอ็นพีแบบยาก (NP-hard) แต่อย่างไรเราสามารถนำขั้นตอนวิธีแบบศึกษาสำนึกมาใช้หาจุดศูนย์กลางของกลุ่มข้อมูลจากการลู่เข้าได้อย่างมีประสิทธิภาพ ซึ่งจะเหมือนกับขั้นตอนวิธีหาค่าคาดหมายสูงสุด (expectation-maximization algorithm) สำหรับแบบจำลองแบบผสม (Mixture Model) ของการแจกแจงปรกติ เนื่องจากทั้งสองขั้นตอนวิธีจะใช้แนวทางกระทำซ้ำการกลั่นกรอง (iterative refinement approach) นอกจากนี้ ทั้งสองขั้นตอนวิธียังใช้จุดศูนย์กลางของคลัสเตอร์สร้างแบบจำลองข้อมูล อย่างไรก็ตาม การจับกลุ่มข้อมูลแบบค่าเฉลี่ย k มีแนวโน้มจะได้คลัสเตอร์ผลลัพธ์ที่มีตำแหน่งขอบเขตใกล้เคียงกัน ในขณะที่ขั้นตอนวิธีหาค่าคาดหมายสูงสุดนั้นยอมให้คลัสเตอร์ผลลัพธ์มีรูปร่างที่แตกต่างกันได้

ขั้นตอนวิธีนี้ไม่มีอะไรเกี่ยวข้องกับขั้นตอนวิธีการค้นหาเพื่อนบ้านใกล้สุด k ตัว ซึ่งเป็นเทคนิคการเรียนรู้ของเครื่องที่เป็นที่นิยมอีกอย่างหนึ่ง

คำอธิบาย

สมมติให้มีเซตของการสังเกต (x₁, x₂, …, x_n) โดยแต่ละการสังเกตเป็นเวกเตอร์ค่าจริงใน d มิติ การจับกลุ่มข้อมูลแบบค่าเฉลี่ย k จะตัดแบ่งการสังเกตจำนวน n ครั้งให้เป็นข้อมูลจำนวน k ชุด (โดยที่ k น้อยกว่าหรือเท่ากับ n) ในเซต S = {S₁, S₂, …, S_k} ที่จะทำให้ค่าผลบวกกำลังสองภายในคลัสเตอร์ (within-cluster sum of squares; WCSS) มีค่าน้อยที่สุด. หรือพูดได้อีกอย่างว่า จุดประสงค์ของการจับกลุ่มข้อมูลแบบค่าเฉลี่ย k คือการหาผลลัพธ์ต่อไปนี้:

$\underset{𝐒}{a r g m i n} \sum_{i = 1}^{k} \sum_{𝐱 \in S_{i}} {‖ 𝐱 - μ_{i} ‖}^{2}$

โดยที่ μ_i เป็นค่าเฉลี่ยของจุดใน S_i

ประวัติ

คำศัพท์ "k-means" ได้ถูกระบุใช้ครั้งแรกโดย James MacQueen ในปี พ.ศ. 2510,^[1] แม้ว่าแนวคิดเริ่มแรกจะเป็นของ Hugo Steinhaus ซึ่งเกิดขึ้นในปี พ.ศ. 2500^[2] และขั้นตอนวิธีมาตรฐานนั้นก็ถูกเสนอขึ้นในปี พ.ศ. 2500 โดย Stuart Lloyd เพื่อเป็นเทคนิคสำหรับการกล้ำรหัสของพัลส์ อย่างไรก็ตามขั้นตอนวิธีไม่ได้ถูกเผยแพร่ออกไปจาก Bell Labs จนกระทั่งปี พ.ศ. 2525^[3] ในปี พ.ศ. 2508 E.W.Forgy ได้ตีพิมพ์วิธีเดียวกันนี้เช่นกัน จึงทำให้บางครั้งวิธีนี้ถูกกล่าวถึงในชื่อ Lloyd-Forgy^[4] นอกจากนี้ได้มีการตีพิมพ์แบบฉบับที่มีการพัฒนาขึ้นไป โดย Hartigan and Wong ในปี พ.ศ. 2518 / 2522^[5]

ขั้นตอนวิธี

ขั้นตอนวิธีมาตรฐาน

ขั้นตอนวิธีที่ใช้มากที่สุดใช้แนวทางกระทำซ้ำการกลั่นกรอง (iterative refinement approach) และถูกเรียกว่า การจับกลุ่มข้อมูลแบบค่าเฉลี่ย k (k-means algorithm) หรือในบางครั้งสามารถพบในชื่อ Lloyd's algorithm โดยเฉพาะในวงการวิทยาการคอมพิวเตอร์ เริ่มด้วยเซตเริ่มต้นประกอบด้วยค่าเฉลี่ย k ค่า m₁⁽¹⁾,…,m_k⁽¹⁾ แล้วจากนั้นจะเป็นการทำซ้ำระหว่างสองขั้นตอน^[6]

ขั้นตอนการกำหนดค่า: กำหนดแต่ละข้อมูลการสังเกตไปยังคลัสเตอร์ โดยเลือกคลัสเตอร์ที่จะทำให้ค่าผลบวกกำลังสองภายในคลัสเตอร์ (within-cluster sum of squares; WCSS) นั้น ๆ มีค่าน้อยที่สุด เนื่องจากผลบวกของค่ากำลังสองเป็นค่ากำลังสองของระยะทางแบบยุคลิด (Euclidean distance) มันจึงเป็นค่าเฉลี่ย “ที่ใกล้ที่สุด”^[7] (โดยทางคณิตศาสตร์ นี่เป็นการแสดงว่าการตัดแบ่งข้อมูลตามแผนภาพโวโรนอย (Voronoi diagram) นั้นแบ่งตามค่าเฉลี่ยข้างต้น)

$S_{i}^{(t)} = {x_{p} : ‖ x_{p} - m_{i}^{(t)} ‖^{2} \leq ‖ x_{p} - m_{j}^{(t)} ‖^{2} \forall j, 1 \leq j \leq k},$

โดยที่ ค่า

x_{p}

แต่ละค่ามีแค่หนึ่งค่า

S^{(t)}

แม้ว่าจะมีค่าที่เป็นไปได้สองค่าขึ้นไป

ขั้นตอนการปรับค่า: คำนวณค่าเฉลี่ยค่าใหม่เพื่อเป็นจุดเซนทรอยด์ (centroid) ของข้อมูลการสังเกตในแต่ละคลัสเตอร์ที่สร้างขึ้นใหม่

$m_{i}^{(t + 1)} = \frac{1}{| S_{i}^{(t)} |} \sum_{x_{j} \in S_{i}^{(t)}} x_{j}$

ซึ่งจะทำให้ค่าผลบวกกำลังสองภายในคลัสเตอร์ใหม่นั้นมีค่าน้อยกว่าเก่า เนื่องจากว่าค่าเฉลี่ยเลขคณิตเป็นตัวประมาณค่ากำลังสองน้อยสุด

จากขั้นตอนข้างต้น ค่าที่ได้จะลู่เข้าหาค่าค่าหนึ่งและไม่มีการเปลี่ยนแปลงในการกำหนดค่าอีก และเนื่องจากทั้งสองขั้นตอนให้ค่า WCSS ที่เหมาะที่สุด และการเลือกแบ่งกลุ่มข้อมูลมีวิธีได้จำกัด ขั้นตอนวิธีนี้จะต้องลู่เข้าหาค่า local optimum ทั้งนี้ทั้งนั้นวิธีนี้ไม่สามารถรับประกันได้ว่าจะพบค่าที่ดีที่สุดที่เป็นไปได้ หรือ global optimum^[8] ขั้นตอนวิธีนี้ถูกใช้บ่อยเพื่อการแจกแจงสิ่งของไปยังกลุ่มที่ใกล้ที่สุดด้วยระยะห่าง ขั้นตอนวิธีมาตรฐานมีจุดมุ่งหมายเพื่อทำให้ค่า WCSS มีค่าน้อยที่สุดที่เป็นไปได้ และใช้ค่ากำลังสองน้อยสุดกำหนดระยะห่าง ซึ่งก็คือ ค่ากำลังสองของระยะทางแบบยุคลิด อย่างไรก็ตาม การเลือกใช้ฟังก์ชันระยะห่างอื่น ๆ นอกเหนือไปจากค่ากำลังสองของระยะทางแบบยุคลิด อาจทำให้ขั้นตอนวิธีนี้ไม่เกิดการลู่เข้า นอกจากนี้มีการแก้ไขเพิ่มเติมของกระบวนการ (modifications of k-means) เช่น ค่าเฉลี่ย k แบบทรงกลม (spherical k-means) และ k-medoids เพื่อทำให้การคำนวณระยะห่างแบบอื่น ๆ ใช้กับขั้นตอนวิธีนี้ได้

วิธีการกำหนดค่าตั้งต้น

โดยทั่วไปแล้ว จะใช้วิธีของ Forgy และวิธีการตัดแบ่งแบบสุ่ม (Random Partition^[9]) เป็นวิธีการกำหนดค่าตั้งต้น วิธีของ Forgy คือการเลือกข้อมูลการสังเกต k อย่างขึ้นมาแบบสุ่ม จากข้อมูลทั้งหมด แล้วใช้เป็นค่าเฉลี่ยเริ่มต้น ส่วนการตัดแบ่งข้อมูลแบบสุ่มนั้นจะเริ่มต้นด้วยการสุ่มจัดข้อมูลการสังเกตแต่ละอันไปอยู่ในกลุ่มใด ๆ และจากนั้นจะทำการปรับค่าตามขั้นตอนที่กล่าวไปแล้ว ดังนั้นค่าเฉลี่ยเริ่มต้นที่ได้จาการปรับค่าจะเป็นจุดเซนทรอยด์ (centroid) ของข้อมูลการสังเกตในแต่ละคลัสเตอร์ที่สร้างขึ้นมาแบบสุ่มนั่นเอง วิธีของ Forgy มีแนวโน้มที่จะกระจายค่าเฉลี่ยเริ่มต้น ในขณะที่การตัดแบ่งข้อมูลแบบสุ่มจะเลือกค่าเริ่มต้นที่ใกล้กับจุดกึ่งกลางของข้อมูลทั้งหมด นอกจากนี้ อ้างอิงจาก Hamerly และคณะ^[9] การตัดแบ่งข้อมูลแบบสุ่มที่เหมาะกับขั้นตอนวิธีการหา k-harmonic means และ fuzzy k-means มากกว่า ในทางกลับกัน สำหรับขั้นตอนวิธีหาค่าคาดหมายสูงสุด หรือขั้นตอนวิธีการหาค่าเฉลี่ย k แบบมาตรฐาน วิธีของ Forgy จะเป็นที่นิยมมากกว่า

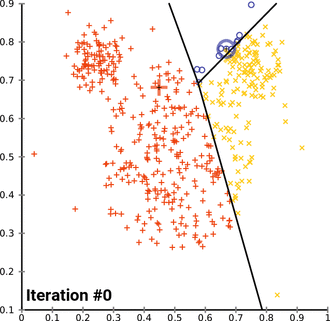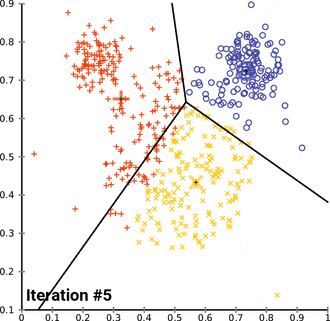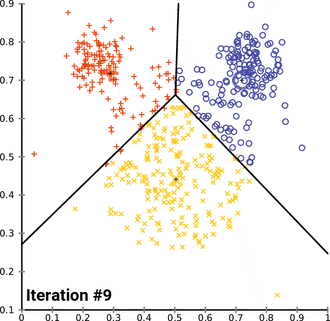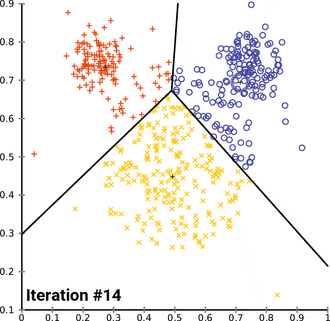
ภาพสาธิตของขั้นตอนวิธีมาตรฐาน
1) เลือกค่าเฉลี่ยเริ่มต้น k (ในกรณีนี้ k=3) แบบสุ่มจากโดเมนข้อมูล
2) สร้างคลัสเตอร์ k กลุ่ม โดยการเชื่อมโยงทุกข้อมูลการสังเกตด้วยค่าเฉลี่ยที่ใกล้ที่สุด เส้นแบ่งในที่นี้แสดงให้เห็นแผนภาพของโวโรนอย (Voronoi diagram) ที่สร้างขึ้นจากค่าเฉลี่ย
3) จุดเซนทรอยด์ของแต่ละคลัสเตอร์กำหนดเป็นค่าเฉลี่ยค่าใหม่
4) ทำซ้ำขั้นตอนที่ 2 และ 3 จนกระทั่งค่ากลางของแต่ละคลัสเตอร์ไม่เปลี่ยนแปลง

เนื่องจากเป็นขั้นตอนวิธีแบบศึกษาสำนึก จึงไม่สามารถรับประกันได้ว่ากระบวนการนี้จะลู่เข้าหา global optimum และการจัดกลุ่มในตอนเริ่มต้น หรือการกำหนดค่าตั้งต้นจะมีผลอย่างมากต่อผลลัพธ์ อย่างไรก็ตามขั้นตอนวิธีนี้สามารถหาผลลัพธ์ได้อย่างรวดเร็ว จึงเป็นเรื่องปรกติที่จะทดสอบข้อมูลหลาย ๆ ครั้งด้วยเงื่อนไขเริ่มต้นที่แตกต่างกัน แต่ในกรณีที่เลวร้ายที่สุดค่าเฉลี่ย k (k-means) อาจจะลู่เข้าอย่างช้า ซึ่งมีความเป็นไปได้แม้แต่กับข้อมูลจำนวนน้อย ๆ และมีการแสดงอย่างเฉพาะเจาะจงว่า สำหรับในบางตัวอย่างข้อมูล ที่มีแค่สองมิติ การหาค่าเฉลี่ย k เป็นขั้นตอนวิธีเวลาแบบเลขชี้กำลัง (exponential time) หรือก็คือ แม่แบบ:Math ในการลู่เข้า^[10] ข้อมูลดังกล่าวเหมือนว่าจะไม่เกิดขึ้นในการปฏิบัติจริง จึงสามารถยืนยันได้ว่า เวลาที่ใช้ในการทำงานที่ปรับเรียบ (smoothed running time) ของขั้นตอนการหาค่าเฉลี่ย k เป็นเป็นฟังก์ชันพหุนาม^[11]

ขั้นตอนการกำหนดค่ามีอีกชื่อหนึ่งคือ ขั้นตอนการคาดหมาย (expectation step) และขั้นตอนการปรับค่าสามารถเรียกว่า ขั้นตอนการหาค่าสูงสุด maximization step ทำให้ขั้นตอนวิธีนี้เป็นส่วนหนึ่งของขั้นตอนวิธีหาค่าคาดหมายสูงสุดแบบทั่วไป (generalized expectation-maximization algorithm)

ความซับซ้อน

เมื่อกล่าวถึงความซับซ้อนเชิงคำนวณ (computational complexity) การหาคำตอบที่เหมาะสม ในการแบ่งข้อมูลแบบค่าเฉลี่ย k สำหรับข้อมูลการสังเกต ใน d มิติ จะเป็น

ปัญหาเอ็นพีแบบยาก (NP-hard) ในปริภูมิแบบยุคลิดทั่วไป (Euclidean space) d แม้กระทั่งสำหรับ 2 กลุ่มข้อมูล^[12]^[13]
ปัญหาเอ็นพีแบบยาก (NP-hard) ในปริภูมิแบบยุคลิดทั่วไป (Euclidean space) d แม้กระทั่งสำหรับ 2 กลุ่มข้อมูล สำหรับจำนวนกลุ่มข้อมูล k แม้กระทั่งในระนาบ^[14]
ถ้ากำหนดค่า k และค่า d คงที่ จะสามารถแก้ปัญหาในเวลา $O (n^{d k + 1} \log n)$ โดยที่ค่า n เป็นจำนวนข้อมูลทั้งหมด^[15]

ดังนั้น ประเภทของขั้นตอนวิธีแบบศึกษาสำนึก เช่น ขั้นตอนวิธีของ Lloyds จึงถูกใช้อย่างแพร่หลาย เวลาที่ใช้ในการทำงานของขั้นตอนวิธีของ Lloyds จะอยู่ในรูป $O (n k d i)$ โดยที่ค่า n เป็นจำนวนของเวกเตอร์ข้อมูล ใน d มิติ ค่า k เป็นจำนวนของคลัสเตอร์ และค่า i เป็นจำนวนของการวนซ้ำจนกระทั่งผลลัพธ์ลู่เข้าและไม่เปลี่ยนแปลง สำหรับข้อมูลที่มีโครงสร้างเป็นกลุ่มก้อน การวนซ้ำในจำนวนรอบน้อย ๆ ก็มักจะเห็นการลู่เข้า และผลลัพธ์จะดีขึ้นเพียงเล็กน้อยเท่านั้นหลังจากการวนซ้ำสิบกว่าครั้ง ดังนั้นขั้นตอนวีธีของ Lloyds ในทางปฏิบัติจะระบุว่ามีความซับซ้อนแบบเชิงเส้น

ส่วนต่อจากนี้จะเป็นความรู้เพิ่มเติมล่าสุดเกี่ยวกับพฤติกรรมความซับซ้อนของขั้นตอนวิธีนี้

ขั้นตอนวิธีการหาค่าเฉลี่ย k ของ Lloyd มีเวลาที่ใช้ในการทำงานปรับเรียบแบบพหุนาม แสดงให้เห็นว่า ^[11] สำหรับเซตของ n จุดใด ๆ ใน $[0, 1]^{d}$ ถ้าแต่ละจุดจะเป็นรบกวนด้วยการแจกแจงปรกติด้วยค่าเฉลี่ย $0$ และค่าความแปรปรวน $σ^{2}$ จากนั้นเวลาที่ใช้ในการทำงานที่คาดหมายไว้ของขั้นตอนวิธีค่าเฉลี่ย k จะอยู่ในขอบเขต $O (n^{34} k^{34} d^{8} l o g^{4} (n) / σ^{6})$ ซึ่งจะเป็นพหุนามในรูป $n$ , $k$ , $d$ และ $1 / σ$

นอกจากนั้นเราสามารถระบุขอบเขตที่ดีขึ้นในกรณีที่เรียบง่าย ตัวอย่างเช่น^[16] เวลาที่ใช้ในการทำงานของขั้นตอนวิธีค่าเฉลี่ย k จะอยู่ในขอบเขต $O (d n^{4} M^{2})$ สำหรับจุดข้อมูล $n$ จุดในแลตทิชจำนวนเต็ม (integer lattice) ${1, \dots, M}^{d}$

รูปแบบที่เปลี่ยนแปลง

Jenks natural breaks optimization: การหาค่าค่าเฉลี่ย k สำหรับข้อมูลตัวแปรเดียว
k-medians clustering ใช้ค่ามัธยฐานในแต่ละมิติของข้อมูลแทนค่าเฉลี่ย และวิธีนี้จะทำให้ค่ากลาง $L_{1}$ มีค่าน้อยที่สุด (Taxicab geometry)
k-medoids (หรือก็คือ Partitioning Around Medoids, PAM) ใช้ตัวแทนของกลุ่มที่เรียกว่า medoid แทนค่าเฉลี่ย และวิธีนี้จะทำให้ผลรวมของระยะห่างสำหรับฟังก์ชันระยะห่างใด ๆ ให้มีค่าน้อยที่สุด
Fuzzy c-means clustering เป็นเวอร์ชันที่ยืดหยุ่นจากการหาค่าเฉลี่ย k โดยที่แต่ละจุดข้อมูลมีดีกรีความคลุมเครือของความเป็นเจ้าของ (fuzzy degree of belonging) กับแต่ละคลัสเตอร์
Gaussian mixture เป็นแบบจำลองจากขั้นตอนวิธีหาค่าคาดหมายสูงสุด (EM algorithm) ที่สนับสนุนการกำหนดค่าตามความน่าจะเป็น (probabilistic assignments) ไปยังคลัสเตอร์ แทนที่จะเป็นการกำหนดค่าชี้เฉพาะ (deterministic assignments) และใช้การแจกแจงปรกติหลายตัวแปร (multivariate Gaussian distributions) แทนที่จะเป็นค่าเฉลี่ย
k-means++ เลือกศูนย์กลางเริ่มต้นที่ให้ค่าขอบเขตบนที่พิสูจน์ได้ในค่ากำลังสองน้อยสุด (WCCS)
ขั้นตอนวิธีการกรองจะใช้ kd-tree ในการเร่งการหาค่าเฉลี่ย k แต่ละขั้นให้เร็วขึ้น^[17]
บางวิธีพยายามเร่งการหาค่าเฉลี่ย k แต่ละขั้นให้เร็วขึ้นด้วย coreset^[18] หรืออสมการสามเหลี่ยม triangle inequality^[19]
ขั้นตอนวิธีนี้สามารถหนีจากค่าเหมาะสมที่สุดเฉพาะที่ด้วยการสลับจุดข้อมูลระหว่างคลัสเตอร์^[20]

ขั้นตอนวิธีการแบ่งกลุ่มแบบ Spherical k-means ซึ่งเหมาะสำหรับข้อมูลที่มีทิศทาง^[21]

Minkowski metric weighted k-means ใช้สำหรับฟีเจอร์ที่ไม่สัมพันธ์กัน โดยการกำหนดค่าน้ำหนักเฉพาะของคลัสเตอร์กับแต่ละฟีเจอร์^[22]

อภิปราย

องค์ประกอบสองอย่างที่ทำให้การแบ่งกลุ่มแบบค่าเฉลี่ย k เป็นขั้นตอนวิธีที่มีประสิทธิภาพ แต่ก็มักจะถูกพิจารณว่าเป็นข้อเสียของการแบ่งกลุ่มแบบค่าเฉลี่ย k ได้แก่:

ระยะทางแบบยูคลิดได้ถูกใช้ให้เป็นตัววัดระยะห่างระหว่างข้อมูลและความแปรปรวน (Variance) ถูกใช้เป็นตัววัดการกระจ่ายของกลุ่มข้อมูล
จำนวนของกลุ่มของข้อมูล k เป็นตัวแปรเสริมที่ถูกนำเข้าในขั้นตอนวิธี: ตัวเลือกที่ไม่เหมาะสมสำหรับค่าของ k อาจจะส่งผลให้ผลลัพธ์ที่ออกมาไม่ดีนัก ดังนั้นการตรวจสอบจำนวนของกลุ่มข้อมูลที่เหมาะสมต่อข้อมูลจึงเป็นสิ่งที่สำคัญอย่างยิ่งก่อนจะเริ่มดำเนินการแบ่งกลุ่มแบบค่าเฉลี่ย k
การลู่เข้าถึงค่าต่ำสุดเฉพาะที่ (local minimum) อาจส่งผลให้ขั้นตอนวิธีมอบผลลัพธ์ที่ผิดพลาดได้

ปัจจัยที่จำกัดความสามารถของการแบ่งกลุ่มแบบค่าเฉลี่ย k คือแบบจำลองของกลุ่มข้อมูล การแบ่งกลุ่มของข้อมูลแบบค่าเฉลี่ย k คาดการณ์แบบจำลองของกลุ่มข้อมูลเป็นรูปแบบของทรงกลม และข้อมูลสามารถถูกแบ่งกลุ่มได้โดยการที่ค่าเฉลี่ยของกลุ่มข้อมูลลู่เข้า ถึงจุดศูนย์กลางของกลุ่มข้อมูลทรงกลมนั้น กลุ่มข้อมูลแต่ละกลุ่มถูกคาดการณ์ไว้ว่าจะมีขนาดที่ใกล้เคียงกัน ทำให้การกำหนดกลุ่มของข้อมูลแต่ละตัวไปยังจุดศูนย์กลางของกลุ่มข้อมูลที่อยู่ใกล้ที่สุดถูกต้อง ซึ่งปัจจัยเหล่านี้ก่อให้เกิดปัญหาในการแบ่งกลุ่มแบบค่าเฉลี่ย k ต่อกลุ่มข้อมูลที่มีลักษณะไม่ตรงไปตามความคาดการณ์ที่ถูกกำหนดไว้ในขั้นตอนวิธี

เราสามารถมองผลลัพธ์ของการแบ่งกลุ่มแบบค่าเฉลี่ย k ได้ในรูปแบบของแผนภาพโวโรนอยของค่าเฉลี่ยกลุ่มข้อมูล เนื่องจากข้อมูลถูกแบ่งครึ่งทางระหว่างระยะห่างของจุดศุนย์กลางของกลุ่มข้อมูลแต่ละกลุ่ม ดังนั้นจึงอาจจะทำให้เกิดการแบ่งข้อมูลที่ไม่เหมาะสมอย่างที่สุดได้ (ดูตัวอย่างใน กลุ่มข้อมูล "mouse") การแจกแจงปรกติซึ่งใช้โดยขั้นตอนวิธีค่าคาดหมายสูงสุด ซึ่งมีความยึดหยุ่นในการแบ่งข้อมูลเนื่องจากมีการคำนวณโดยใช้ทั้งการแปรปรวนและการแปรปรวนร่วมเกี่ยว ส่งผลให้สามารถแบ่งกลุ่มข้อมูลที่มีขนาดแตกต่างกันในแต่ละกลุ่มได้ดีกว่าการแบ่งกลุ่มแบบค่าเฉลี่ย k

การประยุกต์ใช้

การแบ่งกลุ่มแบบค่าเฉลี่ย k เป็นขั้นตอนวิธีที่ง่ายต่อการสร้างและสามารถใช้ได้กับข้อมูลที่มีขนาดใหญ่ ดังนั้นการแบ่งกลุ่มแบบค่าเฉลี่ย k จึงถูกใช้อย่างแพร่หลายในหลายหัวข้อ ยกตัวอย่างเช่น การแบ่งส่วนตลาด, คอมพิวเตอร์วิทัศน์, สถิติ, ดาราศาสตร์ และ เกษตรกรรม. การแบ่งกลุ่มแบบค่าเฉลี่ย k มักถูกใช้เป็นตัวประมวณผลก่อนการเริ่มใช้ขั้นตอนวิธีอื่น ๆ

การแบ่งนับเวกเตอร์

การแบ่งกลุ่มแบบค่าเฉลี่ย k ถูกริเริ่มขึ้นเพื่อใช้ในการประมวลสัญญาณและยังคงถูกใช้มาจนถึงในปัจจุบันนี้ ยกตัวอย่างเช่นในคอมพิวเตอร์กราฟิก, การแบ่งนับสี (Color quantization เป็นกระบวนการของการลดจำนวนชนิดสีในแต่ละภาพให้เหลือเพียงจำนวนสีเท่ากับ k ตามที่ถูกกำหนดไว้ ซึ่งการการแบ่งกลุ่มแบบค่าเฉลี่ย k นี้สามารถนำมาใช้เพื่อปฏิบัติการแบ่งนับสีได้อย่างง่ายดายและมีประสิทธิภาพ การใช้ประโยชน์จากการแบ่งนับเวกเตอร์อย่างอื่นได้แก่การชักตัวอย่างแบบไม่สุ่ม (non-random sampling) ซึ่งการแบ่งกลุ่มแบบค่าเฉลี่ย k ช่วยในการเลือก k ชนิดของข้อมูลที่แตกต่างกันจากจำนวนข้อมูลขนาดใหญ่เพื่อการดำเนินการวิเคราะห์ผลต่อไป

การวิเคราะห์กลุ่มข้อมูล

ในการวิเคราะห์กลุ่มข้อมูล (Cluster Analysis) การแบ่งกลุ่มแบบค่าเฉลี่ย k สามารถถูกนำมาใช้ในการแบ่งชุดข้อมูลป้อนเข้าให้เป็น k ส่วนได้ อย่างไรก็ตามด้วยการแบ่งกลุ่มแบบค่าเฉลี่ย k เพียงอย่างเดียว ไม่ยืดหยุ่นพอที่จะใช้แบ่งกลุ่มข้อมูลได้อย่างมีประสิทธิภาพ โดยเฉพาะอย่างยิ่งความยากในการเลือกค่าของ k ที่เหมาะสมต่อกลุ่มข้อมูล และข้อจำกัดที่การแบ่งกลุ่มแบบค่าเฉลี่ย k นั้นไม่สามารถใช้แบ่งชุดข้อมูลที่ไม่ใช่ตัวเลขได้ ด้วยเหตุนี้ขั้นตอนวิธีอื่น ๆ จึงถูกพัฒนาขึ้นทดแทนการแบ่งกลุ่มแบบค่าเฉลี่ย k เพื่อผลลัพธ์ที่ดีขึ้น

การเรียนรู้ลักษณะเฉพาะ (Feature learning)

การจับกลุ่มข้อมูลแบบค่าเฉลี่ย k ได้ถูกนำไปใช้ในขั้นตอนฟีเจอร์เลิร์นนิ่ง (Feature learning) ทั้งในการเรียนรู้แบบมีผู้สอน (supervised learning) การเรียนรู้แบบกึ่งมีผู้สอน (semi-supervised learning) และการเรียนรู้แบบไม่มีผู้สอน (unsupervised learning)^[23] ขั้นตอนในการปฏิบัติเริ่มจากการสร้างกลุ่มข้อมูลจำนวน k กลุ่มด้วยการจับกลุ่มข้อมูลแบบค่าเฉลี่ย k โดยใช้ข้อมูลสอน (training data) หลังจากนั้นจึงโปรเจกต์ข้อมูลป้อนเข้าไปยังฟีเจอร์สเปซใหม่ โดยใช้แมทริกส์โปรดัคระหว่างข้อมูลและตำแหน่งของศูนย์กลางของแต่ละกลุ่มข้อมูล ระยะห่างระหว่างข้อมูลป้อนเข้าและศูนย์กลางของแต่ละกลุ่มข้อมูล ฟังก์ชันที่ชี้ข้อมูลป้อนเข้าถึงจุดศูนย์กลางของกลุ่มข้อมูลที่ใกล้ที่สุด^[23]^[24] หรือสมูทฟังก์ชันของระยะห่างระหว่างข้อมูลและศูนย์กลางของกลุ่มข้อมูลเป็นต้น^[25]

การใช้งานของการแบ่งกลุ่มแบบค่าเฉลี่ย k นี้ประสบความสำเร็จในร่วมใช้งานกับตัวแยกแบบเชิงเส้น (linear classifier) สำหรับข้อมูลแบบกึ่งมีผู้สอนในการประมวลภาษาธรรมชาติ^[26] และในคอมพิวเตอร์วิทัศน์ โดยเฉพาะอย่างยิ่งในการรู้จำวัตถุ (object recognition) นั้นการจับกลุ่มข้อมูลแบบค่าเฉลี่ย k สามารถให้ผลลัพธ์ที่มีประสิทธิภาพใกล้เคียงกับ วิธีการเรียนรู้ลักษณะเฉพาะที่ซับซ้อนแบบอื่นยกตัวอย่างเช่น ตัวเข้ารหัสอัตโนมัติ และ restricted Boltzmann machines.^[25] อย่างไรก็ตามการจับกลุ่มข้อมูลแบบค่าเฉลี่ย k นั้น ต้องการจำนวนข้อมูลป้อนเข้าที่มีขนาดมากกว่าที่วิธีฟีเจอร์เลิร์นนิ่งที่ซับซ้อนที่กล่าวมาข้างต้นต้องการ เพื่อให้ได้ผลลัพธ์ที่ใกล้เคียงกันเนื่องจากในการจับกลุ่มข้อมูลแบบค่าเฉลี่ย k นั้น ข้อมูลแต่ละอันส่งผลถึงฟีเจอร์เพียงอันเดียวมากกว่าที่จะส่งผลถึงหลาย ๆ ฟีเจอร์^[23]

ความสัมพันธ์กับขั้นตอนวิธีการเรียนรู้ของเครื่องแบบอื่น ๆ

เราสามารถกล่าวได้ว่าการจับกลุ่มข้อมูลแบบค่าเฉลี่ย k และขั้นตอนวิธีค่าคาดหมายสูงสุดนั้นเป็นเพียงแค่เคสพิเศษของการประมาณรูปร่างผสมของเกาส์ (Gaussian mixture model) ดังนั้นโดยปรกติแล้วเราจึงสามารถเปลี่ยนรูปของการจับกลุ่มข้อมูลแบบค่าเฉลี่ย k ให้อยู่ในรูปของรูปร่างผสมของเกาส์ได้^[27] นอกจากรูปร่างผสมของเกาส์แล้ว เรายังสามารถเปลี่ยนรูปของการจับกลุ่มข้อมูลแบบค่าเฉลี่ย k ให้อยู่ในรูปของขั้นตอนวิธีแบบ K-SVD ซึ่งเป็นขั้นตอนวิธีที่คาดการณ์จุดข้อมูลแต่ล่ะจุดในรูปแบบของผลรวมเชิงเส้นของ"เวกเตอร์โค้ดบุ้ค" (codebook vector) โดยที่การจับกลุ่มข้อมูลแบบค่าเฉลี่ย k นั้นมีความข้องเกี่ยวกับกรณีที่ มีการใช้เวกเตอร์โค้ดบุ้คเพียงเวกเตอร์เดียวด้วยค่าน้ำหนักเท่ากับหนึ่งเท่านั้น^[28]

การแบ่งกลุ่มแบบมีนชิฟต์ (Mean shift clustering)

การแบ่งกลุ่มแบบมีนชิฟต์นั้น เป็นขั้นตอนวิธีที่คงจำนวนของข้อมูลในชุดไว้ให้มีขนาดที่เท่ากับจำนวนข้อมูลป้อนเข้าเริ่มต้น ในจุดเริ่มต้นของขั้นตอนวิธีนั้นชุดของข้อมูลนี้เกิดจากการคัดลอกมาจากชุดข้อมูลป้อนเข้า หลังจากนั้นในแต่ละการวนซ้ำข้อมูลในชุดนี้ได้ถูกแทนที่ด้วย ค่าเฉลี่ยของจุดข้อมูลที่อยู่ในชุดที่อยู่ภายในระยะทางที่กำหนดจากจุดข้อมูลจุดนั้น ในทางกลับกันการที่การจับกลุ่มข้อมูลแบบค่าเฉลี่ย k จำกัดการอัปเดตข้อมูลนี้ให้อยู่ที่ข้อมูล k จุดและเปลี่ยนค่าของแต่ละจุดใน k จุดนี้ด้วยค่าเฉลี่ยของจุดข้อมูลทุกจุดที่ในชุดข้อมูลป้อนเข้า ที่อยู่ใกล้กับจุดจุดนั้นที่สุดเมื่อเทียบกับจุดอื่นใน k จุด การแบ่งกลุ่มแบบมีนชิฟต์ที่มีลักษณะคล้ายคลึงกับการแบ่งกลุ่มแบบค่าเฉลี่ย k นั้นเรียกว่า likelihood mean shift ซึ่งในขั้นตอนวิธีนี้มีการแทนที่ค่าของชุดข้อมูลด้วยค่าเฉลี่ยของจุดข้อมูลทั้งหมดในชุดข้อมูลป้อนเข้า ที่มีระยะห่างภายในระยะทางที่กำหนดไว้จากชุดนั้น ๆ^[29] การแบ่งกลุ่มแบบมีนชิฟต์นั้นมีข้อได้เปรียบอย่างหนึ่งเหนือการจับกลุ่มข้อมูลแบบค่าเฉลี่ย k ซึ่งคือ การที่การแบ่งกลุ่มแบบมีนชิฟต์นั้นไม่จำเป็นต้องมีการกำหนดจำนวนของกลุ่มข้อมูลเพราะว่า การแบ่งกลุ่มแบบมีนชิฟต์นั้นจะหาจำนวนของกลุ่มข้อมูลที่จำเป็นโดยอัตโนมัติ แต่อย่างไรก็ตามการแบ่งกลุ่มแบบมีนชิฟต์นั้นใช้เวลาในการประมวลผลนานกว่าการแบ่งกลุ่มแบบค่าเฉลี่ย k มาก

การวิเคราะห์ส่วนประกอบสำคัญ (Principal component analysis)

มีการแสดงให้เห็นใน^[30]^[31]ว่าผลลัพธ์ที่อยู่ในรูปทั่วไปของการจับกลุ่มข้อมูลแบบค่าเฉลี่ย k (ร่วมด้วยตัวบ่งชี้จุดข้อมูลถึงแต่ละกลุ่มข้อมูล) คือผลจากการวิเคราะห์ส่วนประกอบสำคัญ (PCA) และซับสเปซของการวิเคราะห์ส่วนประกอบสำคัญที่ถูกขยายในทิศทางที่สำคัญ กับซับสเปซของศูนย์กลางของกลุ่มข้อมูลที่เกิดจากการแบ่งกลุ่มแบบค่าเฉลี่ย k นั้นเป็นสิ่งเดียวกัน อย่างไรก็ตามการที่การวิเคราะห์องค์ประกอบสำคัญนั้น คือผลลัพธ์โดยทั่วไปของผลลัพธ์จากการแบ่งกลุ่มแบบค่าเฉลี่ย k นั้นไม่ใช่เรื่องใหม่แต่อย่างใด (โปรดดูตัวอย่าง^[32]), และมันก็ตรงไปตรงมาที่จะแสดงให้เห็นถึงตัวอย่างหักล้างกับข้อความที่ว่า ซับสเปซของจุดศูนย์กลางของกลุ่มข้อมูลถูกขยายโดยทิศทางที่สำคัญ^[33]

การวิเคราะห์องค์ประกอบอิสระ (Independent component analysis)

มีการแสดงให้เห็นใน^[34] ว่าภายใต้ข้อกำหนดบางประการและเมื่อข้อมูลป้อนเข้าได้รับการประมวลผลเบื้องค้นด้วยขั้นตอนวิธี whitening transformation การจับกลุ่มข้อมูลแบบค่าเฉลี่ย k นั้นจะให้ผลลัพธ์ที่มีค่าเท่ากับการวิเคราะห์องค์ประกอบอิสระแบบเชิงเส้น

การกรองข้อมูลแบบสองฝ่าย (Bilateral filtering)

การจับกลุ่มข้อมูลแบบค่าเฉลี่ย k มีการอนุมานเอาว่า ลำดับของจุดข้อมูลแต่ละจุดในชุดข้อมูลป้อนเข้านั้นไม่มีผลต่อขั้นตอนวิธี การกรองข้อมูลแบบสองฝ่าย (bilateral filter) นั้นเหมือนกับการจับกลุ่มข้อมูลของค่าเฉลี่ย k ด้วยตรงที่ว่า มันมีการเก็บรักษาชุดของข้อมูลในขณะที่มีการแทนที่ข้อมูลด้วยค่าเฉลี่ยในแต่ละการวนซ้ำ อย่างไรก็ตามการกรองข้อมูลแบบสองฝ่ายจำกัดการคำนวณของค่าเฉลี่ย (แบบ kernel weighted)ให้รวมถึงเพียงแค่จุดข้อมูลที่ใกล้ในลำดับของข้อมูลป้อนเข้า^[29] ด้วยเหตุนี้การกรองข้อมูลแบบสองฝ่ายจึงสามารถนำไปประยุกต์ใช้ได้กับปัญหาเช่นการขจัดสัญญาณรบกวนในรูปภาพ (image denoising) ซึ่งการเรียงตัวของพิกเซลในภาพนั้นมีความสำคัญเป็นอย่างยิ่ง

ขั้นตอนวิธีที่ใกล้เคียง

การจับกลุ่มข้อมูลแบบเคมีดอยด์นั้น มีความใกล้เคียงกับการจับกลุ่มข้อมูลแบบค่าเฉลี่ย k ในด้านของการจับกลุ่มข้อมูลให้อยู่ใน k กลุ่มโดยทำให้ค่าความคลาดเคลื่อนน้อยที่สุด จุดที่แตกต่างกันนั้นคือการที่การจับกลุ่มข้อมูลแบบเคมีดอยด์กำหนดให้ จุดศูนย์กลางของแต่ละกลุ่มข้อมูลเป็นจุดข้อมูลจริง ๆ ที่อยู่ในชุดข้อมูล ไม่ใช่จุดศูนย์กลางที่ถูกคำนวณขึ้นดังเช่นในขั้นตอนวิธีของการจับกลุ่มข้อมูลแบบค่าเฉลี่ย k

ซอฟต์แวร์

ฟรีแวร์/โอเพ่นซอร์ส

แม่แบบ:Div col

Apache Mahout
Apache Spark
CrimeStat
ELKI
Julia
MLPACK (ไลบรารีภาษา C++)
R (ภาษาโปรแกรม)
SciPy
Torch (การเรียนรู้ของเครื่อง)
Weka (การเรียนรู้ของเครื่อง)
OpenCV

แม่แบบ:Div col end

ซอฟต์แวร์เชิงพาณิชย์