ตัวเข้ารหัสอัตโนมัติ

ตัวเข้ารหัสอัตโนมัติ (autoencoder) เป็นขั้นตอนวิธีสำหรับการลดมิติโดยใช้โครงข่ายประสาทเทียมในการเรียนรู้ของเครื่อง วิธีนี้ถูกเสนอครั้งแรกโดยเจฟฟรีย์ ฮินตันในปี 2006^[1]

ภาพรวม

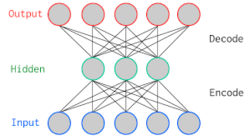
ตัวเข้ารหัสอัตโนมัติเป็นโครงข่ายประสาทเทียมสามชั้นที่ทำการเรียนรู้แบบไม่มีผู้สอนโดยใช้ข้อมูลเดียวกันสำหรับชั้นป้อนเข้าและชั้นขาออก เมื่อข้อมูลการฝึกเป็นมูลค่าจริงและไม่มีการแบ่งเป็นช่วง ฟังก์ชันกระตุ้นของชั้นขาออกมักจะถูกเลือกเป็นฟังก์ชันเอกลักษณ์ (นั่นคือชั้นขาออกเป็นการแปลงเชิงเส้น) หากเราเลือกใช้ฟังก์ชันเอกลักษณะเป็นฟังก์ชันกระตุ้นของชั้นตรงกลาง ผลลัพธ์จะแทบไม่ต่างจากการวิเคราะห์องค์ประกอบหลัก ในทางปฏิบัติวิธีนี้สามารถใช้เพื่อทำการตรวจหาความผิดปกติโดยพิจารณาความแตกต่างระหว่างค่าข้อมูลป้อนเข้าและข้อมูลขาออก

ลักษณะเด่นและข้อจำกัด

ตัวเข้ารหัสอัตโนมัติได้รับการออกแบบให้มีคุณสมบัติที่จำเป็นสำหรับการลดมิติ

โครงสร้างภายในตัวเข้ารหัสอัตโนมัติถูกออกแบบให้จำนวนขนาดของชั้นที่ซ่อนอยู่ $d_{m}$ มีขนาดเล็กกว่าจำนวนของชั้นป้อนเข้าและชั้นขาออก $d_{i, o}$ เนื่องจากว่าถ้าหาก $d_{i, o} ≦ d_{m}$ แล้ว ตัวเข้ารหัสอัตโนมัติจะสามารถทำให้ผิดพลาดในการสร้างใหม่เป็นศูนย์ได้โดยใช้เพียงการแปลงเอกลักษณ์เท่านั้น^[2]

ตัวเข้ารหัสอัตโนมัติสามารถทำการลดมิติข้อมุลลง แต่ไม่ได้หมายความว่าจะสามารถใช้เป็นการเรียนรู้ต้วแทนที่ดีเสมอไป^[3] การลดค่า $d_{m}$ ลงจะทำให้คงไว้แค่ค่าลักษณะที่มีปริมาณข้อมูลมากภายในค่าป้อนเข้า เรียกว่าเป็นการบีบอัดคงข้อมูลหลัก

ทฤษฎี

ได้มีการวิเคราะห์ทางทฤษฎีถึงเหตุผลที่การเข้ารหัสอัตโนมัติสามารถเรียนรู้การสร้างใหม่พร้อมทั้งทำการลดมิติได้

โครงข่ายตัวเข้ารหัสอัตโนมัติ $A E_{ϕ, θ} (x)$ ประกอบขึ้นจากโครงข่ายตัวเข้ารหัส $N N_{ϕ} (x)$ และโครงข่ายตัวถอดรหัส $N N_{θ} (x)$ ในการตีความเชิงกำหนด AE จะให้ข้อมูลที่สร้างขึ้นใหม่จากข้อมูลขาเข้าที่ป้อนเข้าไปโดยตรง นั่นคือ $\hat{x} = A E_{ϕ, θ} (x) = N N_{θ} (N N_{ϕ} (x))$

การตีความเชิงความน่าจะเป็น

ตัวเข้ารหัสอัตโนมัติถือได้ว่าเป็นแบบจำลองตัวแปรแฝงเชิงลึกประเภทหนึ่งจากมุมมองของ แบบจำลองความน่าจะเป็น และสามารถเขียนเป็นสูตรได้ดังต่อไปนี้

\begin{matrix} z_{| x} \sim p_{ϕ} (Z | X) & = p (Z | λ = N N_{ϕ} (X)) = δ (Z - N N_{ϕ} (X)) \\ {\hat{x}}_{| z} \sim p_{θ} (\hat{X} | Z) & = p (\hat{X} | μ = N N_{θ} (Z)) \end{matrix}

นั่นคือสามารถอธิบายได้ว่า $N N_{ϕ} (x), N N_{θ} (x)$ จะให้ค่าพารามิเตอร์การแจกแจง $λ, μ$ และได้ค่า $z, \hat{x}$ โดยการแจกแจง^[4]^[5] เมื่อใช้ $N N_{ϕ} (x), N N_{θ} (x)$ ร่วมกันภายในตัวเข้ารหัสอัตโนมัติสามารถแสดงได้ในรูปนิพจน์ความน่าจะเป็นดังต่อไปนี้:

{\hat{x}}_{| x} \sim p (\hat{X} | μ = A E_{ϕ, θ} (X))

ฟังก์ชันการสูญเสียต่าง ๆ รวมถึงค่าคลาดเคลื่อนกำลังสองเฉลี่ย (MSE, L₂) ถูกนำมาใช้เชิงประจักษ์ (จากมุมมองที่กำหนด) สำหรับการเรียนรู้ของตัวเข้ารหัสอัตโนมัติ ผลที่ได้เป็นเพียงเชิงประจักษ์และไม่อาจรับประกันได้ว่าการเรียนรู้จะสิ้นสุดโดยลู่เข้าเสมอไป

แบบจำลองการแจกแจงแบบปรกติความแปรปรวนคงที่

เมื่อพิจารณาการแจกแจงแบบปกติที่มีความแปรปรวนคงที่ $N (X | μ_{θ}, σ)$ ค่าลบของลอการิทึม ภาวะน่าจะเป็น $L_{n} (θ)$ จะได้เป็น:

L_{n} (θ) = \frac{‖ x - μ_{θ} ‖^{2}}{2 σ^{2}} - \log (\sqrt{2 π σ^{2}}) \propto ‖ x - μ_{θ} ‖^{2}

ซึ่งสามารถตีความได้ว่าเป็นค่าคลาดเคลื่อนกำลังสองของ $x$ และ $μ_{θ}$ นั่นคือการทำให้ค่าลบของลอการิทึมภาวะน่าจะเป็นของ $N (X | μ_{θ} = A E_{ϕ, θ} (x), σ)$ มีค่าต่ำสุด ถือได้ว่าเทียบเท่ากับการทำให้ค่าคลาดเคลื่อนกำลังสองของ $\hat{x} = A E_{ϕ, θ} (x)$ มีค่าต่ำสุด^[6] กล่าวอีกนัยหนึ่งคือ แบบจำลองการเข้ารหัสอัตโนมัติที่ได้รับการฝึกให้เรียนรู้โดยมีค่าคลาดเคลื่อนกำลังสองสามารถมองได้ว่าเป็น แบบจำลองสุ่มตัวอย่างค่าความถี่สูงสุดจากการแจกแจงแบบปรกติความแปรปรวนคงที่ซึ่งถูกประมาณว่าภาวะน่าจะเป็นสูงสุด $N (X | μ_{θ} = A E_{ϕ, θ} (x), σ)$

อ้างอิง

แม่แบบ:รายการอ้างอิง

↑ แม่แบบ:Cite journal
↑ "autoencoder where Y is of the same dimensionality as X (or larger) can achieve perfect reconstruction simply by learning an identity mapping." Vincent. (2010). Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion.
↑ "The criterion that representation Y should retain information about input X is not by itself sufficient to yield a useful representation." Vincent. (2010). Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion.
↑ "a deterministic mapping from X to Y, that is, ... equivalently $q (Y | X; θ) = δ (Y - f_{θ} (X))$ ... The deterministic mapping $f_{θ}$ that transforms an input vector $𝒙$ into hidden representation $𝒚$ is called the encoder." Vincent. (2010). Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion.
↑ " $𝒛 = g_{θ^{'}} (𝒚)$ . This mapping $g_{θ^{'}}$ is called the decoder. ... In general $𝒛$ is not to be interpreted as an exact reconstruction of $𝒙$ , but rather in probabilistic terms as the parameters (typically the mean) of a distribution $p (X | Z = 𝒛)$ " Vincent. (2010). Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion.
↑ " $g_{θ^{'}}$ is called the decoder ... $Z = g_{θ^{'}} (𝒚)$ ... associated loss function $L (𝒙, 𝒛)$ ... $X | 𝒛 \sim N (𝒛, σ^{2} 𝑰)$ ... This yields $L (𝒙, 𝒛) = L_{2} (𝒙, 𝒛) = C (σ^{2}) ‖ 𝒙 - 𝒛 ‖^{2}$ ... This is the squared error objective found in most traditional autoencoders." Vincent. (2010). Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion.

[hinton2006-1] แม่แบบ:Cite journal

[2] "autoencoder where Y is of the same dimensionality as X (or larger) can achieve perfect reconstruction simply by learning an identity mapping." Vincent. (2010). Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion.

[3] "The criterion that representation Y should retain information about input X is not by itself sufficient to yield a useful representation." Vincent. (2010). Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion.

[4] "a deterministic mapping from X to Y, that is, ... equivalently $q (Y | X; θ) = δ (Y - f_{θ} (X))$ ... The deterministic mapping $f_{θ}$ that transforms an input vector $𝒙$ into hidden representation $𝒚$ is called the encoder." Vincent. (2010). Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion.

[5] " $𝒛 = g_{θ^{'}} (𝒚)$ . This mapping $g_{θ^{'}}$ is called the decoder. ... In general $𝒛$ is not to be interpreted as an exact reconstruction of $𝒙$ , but rather in probabilistic terms as the parameters (typically the mean) of a distribution $p (X | Z = 𝒛)$ " Vincent. (2010). Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion.

[6] " $g_{θ^{'}}$ is called the decoder ... $Z = g_{θ^{'}} (𝒚)$ ... associated loss function $L (𝒙, 𝒛)$ ... $X | 𝒛 \sim N (𝒛, σ^{2} 𝑰)$ ... This yields $L (𝒙, 𝒛) = L_{2} (𝒙, 𝒛) = C (σ^{2}) ‖ 𝒙 - 𝒛 ‖^{2}$ ... This is the squared error objective found in most traditional autoencoders." Vincent. (2010). Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion.

[1]

[2]

[3]

[4]

[5]

[6]

ตัวเข้ารหัสอัตโนมัติ

เนื้อหา

ภาพรวม

ลักษณะเด่นและข้อจำกัด

ทฤษฎี

การตีความเชิงความน่าจะเป็น

แบบจำลองการแจกแจงแบบปรกติความแปรปรวนคงที่

อ้างอิง

รายการนำทางไซต์

ตัวเข้ารหัสอัตโนมัติ

ภาพรวม

ลักษณะเด่นและข้อจำกัด

ทฤษฎี

การตีความเชิงความน่าจะเป็น

แบบจำลองการแจกแจงแบบปรกติความแปรปรวนคงที่

อ้างอิง

รายการนำทางไซต์

ค้นหา