สมการแฟรแนล

คลื่นที่เกิดการสะท้อนและการหักเหเมื่อแผ่จากตัวกลางที่มีดรรชนีหักเหต่ำไปสูง

สมการแฟรแนล (แม่แบบ:Langx, แม่แบบ:Langx) หรือ สัมประสิทธิ์แฟรแนล (แม่แบบ:Langx) เป็นชุดของสมการในทางทัศนศาสตร์ซึ่งค้นพบและอธิบายโดยนักฟิสิกส์ชาวฝรั่งเศส โอกุสแต็ง-ฌ็อง แฟรแนล เพื่ออธิบายการสะท้อน และ การหักเห ของแสงเมื่อแผ่ผ่านตัวกลางสองชนิดที่มีค่าดรรชนีหักเหต่างกัน การสะท้อนที่อธิบายโดยสมการนี้อาจเรียกอีกอย่างว่า "การสะท้อนแบบแฟรแนล"

ภาพรวม

เมื่อแสงเดินทางจากตัวกลางที่มีดรรชนีหักเหเป็น $n_1$ไปยังตัวกลางอีกตัวที่มีดรรชนีหักเหเป็น $n_2$จะเกิดการสะท้อนและหักเหของแสงขึ้นพร้อมกันที่จุดรอยต่อของตัวกลางทั้งสอง สมการแฟรแนลสามารถอธิบายว่าองค์ประกอบต่าง ๆ ของคลื่นแสงจะถูกหักเหและสะท้อนอย่างไร และยังอธิบายถึงการเปลี่ยนแปลงเฟส เมื่อคลื่นสะท้อนกลับ

เงื่อนไขสำหรับสมการคือ: ผิวจุดเปลี่ยนเป็นระนาบเรียบ (ไม่ขรุขระ) และแสงที่ตกกระทบเป็นคลื่นระนาบ

โพลาไรเซชัน s และ p

ผลการคำนวณขึ้นอยู่กับสถานะโพลาไรเซชัน ของแสงที่ตกกระทบ โดยจะแบ่งออกเป็นสองกรณี คือ

1. เมื่อองค์ประกอบสนามไฟฟ้าของแสงตกกระทบโพลาไรซ์ตั้งฉากกับระนาบที่เกิดจากแสงตกกระทบและแสงสะท้อน สถานะของแสงที่ตกกระทบในที่นี้เรียกว่า "คลื่น s" โดย s มาจากภาษาเยอรมัน "senkrecht " แปลว่า "ตั้งฉาก"
2. เมื่อองค์ประกอบสนามไฟฟ้าของแสงตกกระทบโพลาไรซ์ขนานกับระนาบที่เกิดจากแสงตกกระทบและแสงสะท้อน สถานะของแสงที่ตกกระทบในที่นี้เรียกว่า "คลื่น p" โดย p มาจากคำว่า "parallel " ในภาษาเยอรมัน แปลว่า "ขนาน"

อนึ่ง ตั้งฉากและขนานในที่นี้กล่าวถึงทิศทางขององค์ประกอบสนามไฟฟ้าเท่านั้น ส่วนองค์ประกอบสนามแม่เหล็กจะถูกกำหนดตามมาโดยกฎมือขวา

ภาพประกอบแสดงตัวแปรที่ใช้ในสมการแฟรแนล ผิวรอยต่อ (interface) แสดงในแนวตั้ง ส่วนแนวฉาก (normal) เป็นแนวนอน

สมการความเข้มแสง

ในภาพด้านขวา เมื่อแสงตกกระทบ PO มาถึงจุด O บนส่วนรอยต่อระหว่างตัวกลางทั้งสอง แสงส่วนหนึ่งจะสะท้อนไปทาง OQ ในขณะที่อีกส่วนหักเหไปทาง OS ให้มุมระหว่างเส้นแนวฉากกับรังสีตกกระทบ, รังสีสะท้อน และรังสีหักเหเป็น ${\theta }_i$, ${\theta }_r$ และ ${\theta }_t$ตามลำดับ

มุมของรังสีตกกระทบจะเท่ากับมุมของรังสีสะท้อนตามกฎการสะท้อน:

${\theta }_{\mathrm{i}}={\theta }_{\mathrm{r}}$

และความสัมพันธ์ระหว่างมุมตกกระทบกับมุมของรังสีหักเหเป็นไปตามกฎของสแน็ล คือ:

$\frac{\sin {\theta }_{\mathrm{i}}}{\sin {\theta }_{\mathrm{t}}}=\frac{n_2}{n_1}$

อัตราส่วนของความเข้มของแสงที่สะท้อนต่อแสงที่ตกกระทบบนพื้นผิวคือค่า ความสะท้อน $R$ ส่วนอัตราส่วนของการแสงที่หักเหคือค่า ความส่งผ่าน $T$ การคำนวณค่าความสะท้อนและความส่งผ่านต้องใช้ทฤษฎีการแผ่คลื่นแม่เหล็กไฟฟ้า ในวิชาพลศาสตร์ไฟฟ้า รายละเอียดอาจอ่านได้ที่ "หลักการทางทัศนศาสตร์: ทฤษฎีแม่เหล็กไฟฟ้าของการแผ่ของแสง การแทรกสอด และการเลี้ยวเบน" ของ มัคส์ บอร์น หรือ "กลศาสตร์ไฟฟ้าพลศาสตร์แบบคลาสสิก" ของแจ็กสัน

รูปแบบเฉพาะของการสะท้อนแสงและการส่งผ่านยังเกี่ยวข้องกับโพลาไรเซชันของแสงที่ตกกระทบ ถ้าเวกเตอร์องค์ประกอบสนามไฟฟ้าของแสงที่ตกกระทบตั้งฉากกับระนาบของภาพ (คือคลื่น s) ความสะท้อนจะเป็น

$R_s={\left[\frac{\sin ({\theta }_t-{\theta }_i)}{\sin ({\theta }_t+{\theta }_i)}\right]}^2={\left(\frac{n_1\cos {\theta }_i-n_2\cos {\theta }_t}{n_1\cos {\theta }_i+n_2\cos {\theta }_t}\right)}^2={\left[\frac{n_1\cos {\theta }_i-n_2\sqrt{1-{(\frac{n_1}{n_2}\sin {\theta }_i)}^2}}{n_1\cos {\theta }_i+n_2\sqrt{1-{(\frac{n_1}{n_2}\sin {\theta }_i)}^2}}\right]}^2$

ในที่นี้มุมของรังสีหักเห ${\theta }_t$ ถูกแทนด้วยมุมของรังสีตกกระทบ ${\theta }_i$ โดยกฎของสแน็ล แล้วแปลงด้วยเอกลักษณ์ตรีโกณมิติ

ถ้าเวกเตอร์องค์ประกอบสนามไฟฟ้าของแสงที่ตกกระทบขนานกับระนาบของภาพ (คือคลื่น p) ความสะท้อนจะเป็น

$R_p={\left[\frac{\tan ({\theta }_t-{\theta }_i)}{\tan ({\theta }_t+{\theta }_i)}\right]}^2={\left(\frac{n_1\cos {\theta }_t-n_2\cos {\theta }_i}{n_1\cos {\theta }_t+n_2\cos {\theta }_i}\right)}^2={\left[\frac{n_1\sqrt{1-{(\frac{n_1}{n_2}\sin {\theta }_i)}^2}-n_2\cos {\theta }_i}{n_1\sqrt{1-{(\frac{n_1}{n_2}\sin {\theta }_i)}^2}+n_2\cos {\theta }_i}\right]}^2$

ไม่ว่าในกรณีใด ค่าความส่งผ่านจะได้เป็น $T=1-R$

หากแสงที่ตกกระทบเป็นแสงไม่โพลาไรซ์ (ประกอบด้วย ส่วน s และ ส่วน p ในปริมาณที่เท่ากัน) ค่าความสะท้อนโดยรวมคือค่าเฉลี่ยเลขคณิตของทั้งสอง

$R=\frac{R_s+R_p}{2}$

อัตราส่วนของแอมพลิจูดของคลื่นแสงที่สะท้อนและหักเหต่อแอมพลิจูดของคลื่นแสงที่ตกกระทบ จะหาได้จากสมการที่คล้ายกัน แอมพลิจูดการสะท้อนและแอมพลิจูดการส่งผ่านมักจะเขียนด้วยตัวพิมพ์เล็ก $r$ และ $t$ โดยมีความสัมพันธ์กับค่าความสะท้อน $R$ และความส่งผ่าน $T$ คือ:

$R=r^2$

และ

$T=\left(\frac{n_2\cos {\theta }_t}{n_1\cos {\theta }_i}\right)t^2$ 

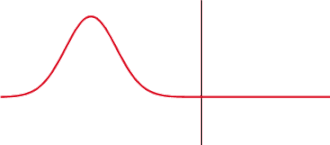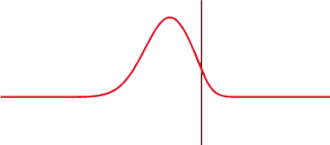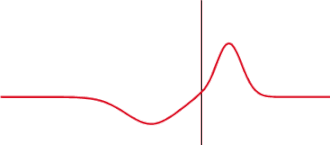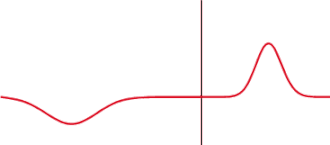
สำหรับแสงตกกระทบที่เป็นคลื่น p ค่า $R_p$จะเป็นศูนย์ที่มุมตกกระทบเป็นค่าจำเพาะค่าหนึ่ง ในกรณีนี้คลื่น p จะถูกส่งผ่านอย่างสมบูรณ์โดยไม่มีการสะท้อนออกมา มุมนี้เรียกว่า มุมบริวสเตอร์ สำหรับกรณีที่ตัวกลางเป็นแก้วในอากาศหรือในสุญญากาศมุมนี้จะมีค่าประมาณ 56° อย่างไรก็ตาม คำจำกัดความนี้ใช้ได้สำหรับตัวกลางที่มีดรรชนีหักเหเป็นจำนวนจริงเท่านั้น สำหรับวัสดุที่ดูดกลืนแสง เช่น โลหะ และ สารกึ่งตัวนำ ดรรชนีหักเหจะเป็นจำนวนเชิงซ้อน ดังนั้น $R_p$ โดยทั่วไปไม่เป็นศูนย์

เมื่อแสงแผ่จากตัวกลางที่มีดรรชนีหักเหสูงไปยังตัวกลางที่มีดรรชนีหักเหต่ำกว่า (คือ $n_1>n_2$) จะมีค่ามีมุมตกกระทบวิกฤต ซึ่งแสงที่ตกกระทบมากกว่ามุมตกกระทบนี้จะถูกสะท้อนโดยพื้นผิวอย่างสมบูรณ์ทั้งคลื่น s และ p นั่นคือ $R_s=R_p=1$ ปรากฏการณ์นี้เรียกว่า การสะท้อนกลับทั้งหมด ค่ามุมวิกฤตนี้มีค่าประมาณ 41° สำหรับแก้วในอากาศ

เมื่อรังสีตกกระทบทำมุมเกือบตั้งฉาก (${\theta }_i\approx {\theta }_t\approx 0$) ความสะท้อนและความส่งผ่านจะเป็น:

$R=R_s=R_p={\left(\frac{n_1-n_2}{n_1+n_2}\right)}^2$

$T=T_s=T_p=1-R=\frac{4n_1{n}_2}{{(n_1+n_2)}^2}$

สำหรับแก้วธรรมดา ค่าความสะท้อนจะอยู่ที่ประมาณ 4% อย่างไรก็ตาม การสะท้อนของคลื่นแสงข้างหน้าต่างรวมถึงชั้นด้านหน้าและชั้นด้านหลัง ดังนั้นคลื่นแสงจำนวนเล็กน้อยจะสะท้อนไปมาระหว่างชั้นทั้งสองก่อให้เกิดการแทรกสอดขึ้น หากละเลยผลของการแทรกสอดนี้ ความสะท้อนรวมของทั้งสองชั้นคือ

$\frac{2R}{1+R}$

หมายเหตุว่า คำอธิบายทั้งหมดในข้างต้นนี้ถือว่าค่าสภาพให้ซึมผ่านได้ทางแม่เหล็กของตัวกลาง $\mu$ มีค่าเท่ากับสภาพให้ซึมผ่านได้ของสุญญากาศ ${\mu }_0$ ซึ่งโดยทั่วไปแล้วจะเป็นจริงสำหรับวัสดุไดอิเล็กตริกส่วนใหญ่ แต่ไม่ใช่สำหรับสสารโดยทั่วไป ดังนั้น รูปแบบของสมการแฟรแนลที่ใช้จริงจึงซับซ้อนยิ่งกว่านี้

ดูเพิ่ม

• แม่แบบ:Cite book
• แม่แบบ:Cite book