ไฮเพอร์โบลา

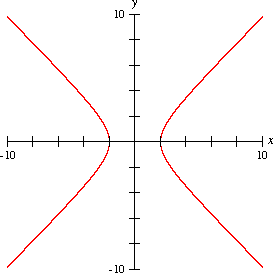
ไฮเพอร์โบลา

ไฮเพอร์โบลา (hyperbola) เป็นเส้นโค้งรูปแบบหนึ่งที่ถูกนิยามในปริภูมิแบบยุคลิด สองมิติ ℝ² เป็นคำทั่วไปสำหรับเรียกเส้นโค้งที่มีระยะห่าง จากจุดสองจุด F และ F' ซึ่งเรียกว่า จุดโฟกัส เป็นค่าคงที่ โดยเส้นตรงที่ลากผ่านทั้งจุดโฟกัสทั้งสองนี้ และเส้นตรงตั้งฉากที่ลากแบ่งครึ่งกลางจุดโฟกัสทั้งสองนี้ จะเรียกว่า แกนหลัก

สมการไฮเพอร์โบลา

ส่วนประกอบทั่วไปในไฮเพอร์โบลา

สมการทั่วไป	$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$	$\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1$
เส้นกำกับ	$\frac{x}{a}\pm \frac{y}{b}=0$	$\frac{x}{a}\pm \frac{y}{b}=0$
จุดโฟกัส	$(\pm \sqrt{a^2+b^2},0)$	$(0,\pm \sqrt{a^2+b^2})$
จุดยอด	$(\pm a,0)$	$(0,\pm b)$
เส้นบังคับ	$x=\pm \frac{a^2}{\sqrt{a^2+b^2}}$	$y=\pm \frac{b^2}{\sqrt{a^2+b^2}}$
ความเยื้องศูนย์กลาง	$e=\frac{\sqrt{a^2+b^2}}{a}$	$e=\frac{\sqrt{a^2+b^2}}{b}$

ไฮเพอร์โบลาสามารถแสดงด้วยสมการต่อไปนี้ในระบบพิกัดคาร์ทีเซียนซึ่งมีแกนพิกัดเป็นแกนหลัก

$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

ในกรณีนี้ พิกัดของจุดโฟกัสอยู่ที่

$F(-\sqrt{a^2+b^2},0)$ และ $F^{\prime }(+\sqrt{a^2+b^2},0)$

และผลต่างของระยะทาง |PF - PF'| จากจุดโฟกัสสองจุด F, F' ไปยังจุด P บนไฮเพอร์โบลาคือ 2a จุดกำเนิดเรียกว่าจุดศูนย์กลางของไฮเพอร์โบลา และจุดสองจุด (±a, 0) เรียกว่าจุดยอดของไฮเพอร์โบลา

ระยะห่าง PF ระหว่างจุด P บนไฮเพอร์โบลากับจุดโฟกัส F และระยะห่างจากจุด P ไปยังเส้นบังคับ (directrix) $x=\frac{a^2}{\sqrt{a^2+b^2}}$ นั้นเป็นอัตราส่วนคงตัว โดยค่าของอัตราส่วนเทียบเท่ากับ ความเยื้องศูนย์กลาง $e=\frac{\sqrt{a^2+b^2}}{a}$

นอกจากนี้ ไฮเพอร์โบลาประกอบด้วย เส้นกำกับ (asymptote) สองเส้น โดยสมการเส้นกำกับคือ

$\frac{x}{a}+\frac{y}{b}=0$ และ $\frac{x}{a}-\frac{y}{b}=0$

ในกรณีเฉพาะเมื่อเส้นกำกับทั้งสองตั้งฉากกัน นั่นคือ a = b ไฮเพอร์โบลาจะเรียกเฉพาะเจาะจงว่า ไฮเพอร์โบลามุมฉาก (rectangular hyperbola)

กราฟของสมการแปรผกผัน แม่แบบ:Math ก็ถือเป็นไฮเพอร์โบลามุมฉากชนิดหนึ่ง

ไฮเพอร์โบลาสามารถทำเป็นสมการอิงตัวแปรเสริมโดยใช้ฟังก์ชันไฮเพอร์โบลิก

$\{\begin{array}{c}x=\pm a\cosh t\\ y=b\sinh t\end{array}$

ไฮเพอร์โบลาบนทรงกรวย

ไฟล์:Conic sections 2.png

ภาคตัดกรวย 4 ประเภท (พาราโบลา, วงรี, วงกลม, ไฮเพอร์โบลา)

ไฮเพอร์โบลาคือขอบเขตของระนาบตัดของกรวยด้านขวาที่ตัดโดยระนาบที่ไม่ผ่านปลายยอดของกรวยด้านขวา แต่ตัดทั้งกรวยบนและล่างขวา

ให้ C_e เป็นภาคตัดกรวย ที่มี ความเยื้องศูนย์กลางเป็น e ในที่นี้ ถ้า e > 1 แล้ว C_e จะกลายเป็นไฮเพอร์โบลา สมมติว่าเส้นบังคับคือ x = -f และหนึ่งในจุดโฟกัสคือ F(f ,0) สำหรับจุด P(x, y) ใด ๆ ของไฮเพอร์โบลา จะได้ว่า

$e(x-f)=\mathrm{P}\mathrm{F}$

โดย $\mathrm{P}\mathrm{F}=\sqrt{(x-f{)}^2+y^2}$ ดังนั้น ทำการยกกำลังสองทั้งสองข้างของสมการข้างต้น และจัดรูปใหม่ได้เป็น

$x^2+2\left(\frac{e^2+1}{e^2-1}\right)fx-\frac{y^2}{e^2-1}=-f^2$

จากนั้นจัดรูปใหม่ทำให้เป็นกำลังสองสมบูรณ์

${(x+\left(\frac{e^2+1}{e^2-1}\right)f)}^2-\frac{y^2}{e^2-1}={\left(\frac{2e}{e^2-1}f\right)}^2$

นี่เป็นรูปแบบพื้นฐานของไฮเพอร์โบลาบนทรงกรวย จากนั้นทำการแปลงเพิ่มเติม $X=x+\frac{e^2+1}{e^2-1}f$, Y= y แล้วจัดเรียงใหม่ให้เหมาะสมก็จะได้รูปสมการดังที่กล่าวข้างต้น

อ้างอิง

• แม่แบบ:Cite book
• แม่แบบ:Cite book